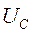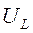Вынужденные электрические колебания

Чтобы вызвать вынужденные колебания, нужно оказать на систему внешнее периодически изменяющееся воздействие. В случае электрических колебаний это можно осуществить, если включить последовательно с элементами контура переменную э.д.с. Или, разорвав контур, подать на образовавшиеся контакты переменное напряжение (рис. 20):

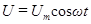. (81)

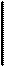
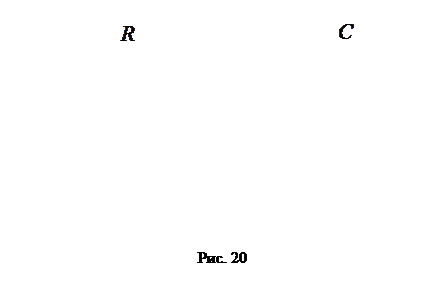
Это напряжение нужно прибавить к э.д.с. самоиндукции. В результате формула (69) примет вид

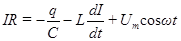. (82)

Произведя преобразования, получим уравнение

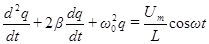. (83)

Уравнение (83) совпадает с дифференциальным уравнением вынужденных механических колебаний (46), где роль 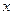выполняет 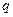, а роль 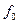выполняет 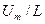. Частное решение уравнения (83) имеет вид

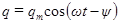, (84)

где

, .

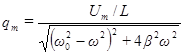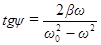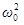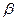Подстановка значений и дает:

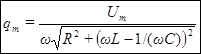, (85)

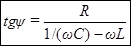. (86)

Общее решение получится, если к частному решению (84) прибавить решение соответствующего однородного уравнения (72), которое по прошествии достаточного времени становиться очень малым и им можно пренебречь. Следовательно, установившиеся вынужденные колебания описываются функцией (84).

Продифференцировав выражение (84) по времени, найдем силу тока в контуре при установившихся колебаниях:

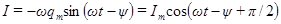
Запишем это выражение в виде

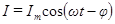, (87)

где 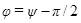есть сдвиг по фазе между током и приложенным напряжением (81). В соответствии с (86)

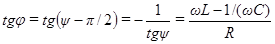. (88)

Из этой формулы следует, что ток отстаёт по фазе от напряжения (φ > 0) в том случае, когда 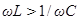и опережает напряжение ( 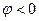) при условии, что 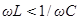. Согласно (85)

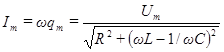. (89)

Представим соотношение (82) в виде

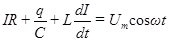. (90)

Произведение 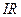равно напряжению 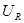на активном сопротивлении, 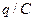есть напряжение на конденсаторе 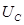, выражение 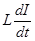определяет напряжение на индуктивности 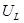. С учетом этого можно написать

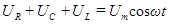. (91)

Таким образом, сумма напряжений на отдельных элементах контура равна в каждый момент времени напряжению, приложенному извне (см. рис.20).

В соответствии с (87)

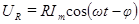(92)

Разделив выражение (84) на электроёмкость, получим напряжение на конденсаторе

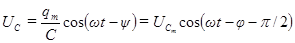. (93)

Здесь

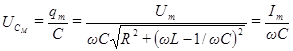. (94)

Умножив производную функции (87) на 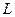, получим напряжение на индуктивности:

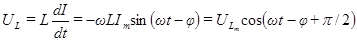.(95)

Здесь

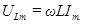. (96)

Сопоставление формул (87), (92), (93), (95) показывает, что напряжение на электроёмкости отстаёт по фазе от силы тока на 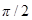. Напряжение на активном сопротивлении изменяется в фазе с током. Фазовые соотношения можно представить очень наглядно с помощью векторной диаграммы. Напомним, что гармоническое колебание (или гармоническую функцию) можно задать с помощью вектора, длина которого равна амплитуде колебания, а направление вектора образует с некоторой осью угол, равный начальной фазе колебаний. Возьмем в качестве прямой, от которой отсчитывается начальная фаза, ось токов. Тогда получается диаграмма, изображенная на рис.21. Согласно (91), три функции 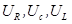в сумме должны быть равны приложенному напряжению 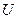. В соответствии с этим напряжение 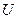изображается на диаграмме вектором, равным сумме векторов 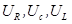. Из прямоугольного треугольника этой диаграммы легко получить следующие выражения для 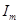и :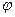

,

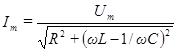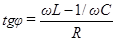
Нетрудно видеть, что эти выражения совпадают с формулами (88) и (89).

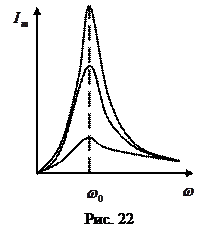
Рассмотрим явление резонанса в случае вынужденных электрических колебаний. Напомним, что резонансом называется резкое возрастание амплитуды колебаний при определённой частоте внешнего напряжения (внешнего периодического воздействия). Резонансными кривыми называют зависимости амплитуды колебаний от частоты внешнего воздействия (в случае электрических колебаний от частоты внешнего напряжения).

Резонансные кривые для силы тока показаны на рис.22. Как видно из выражения (89), амплитуда силы тока имеет максимальное значение при ( 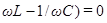. Следовательно, резонансная частота для силы тока совпадает с собственной частотой контура:

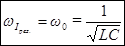. (97)

Максимум при резонансе оказывается тем выше и острее, чем меньше коэффициент затухания .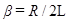

Резонансная частота для заряда 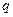и напряжения на конденсаторе 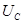равна:

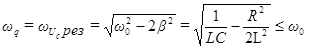(98)

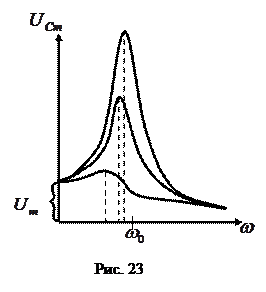
Резонансные кривые для 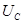изображены на рис. 23 (резонансные кривые для 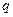имеют такой же вид). При 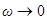резонансные кривые сходятся в одной точке с ординатой 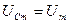, равной напряжению, возникающему на конденсаторе при подключении его к источнику постоянного напряжения 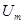. Максимум при резонансе получается тем выше и острее, чем меньше 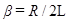, т.е. чем меньше активное сопротивление и больше индуктивность контура. При малом затухании 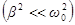резонансную частоту для напряжения можно положить равной 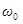. Соответственно можно считать, что 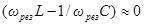. Согласно формуле (94), отношение амплитуды напряжения на конденсаторе при резонансе к амплитуде внешнего напряжения будет в этом случае равно:

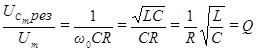(99)

Мы положили в формуле (94) 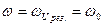. Таким образом, добротность показывает, во сколько раз напряжение на конденсаторе может превысить приложенное напряжение.

Добротность контура связана и с другой важной характеристикой резонансной кривой – её шириной. Оказывается, при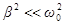

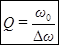(100)

где 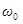- резонансная частота, 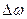– ширина резонансной кривой на “высоте”, равной 0,7 от максимальной, т.е. в резонансе.

Итак, явление резонанса в нашем случае – это возбуждение колебаний с большой амплитудой при частоте внешнего напряжения, равной или близкой к собственной частоте колебательного контура. Резонанс используется для выделения из сложного напряжения нужной составляющей. На этом основана вся техника радиоприёма.

С явлением резонанса связана и опасность: внешнее напряжение или э.д.с. могут быть малы, однако при этом напряжения на отдельных элементах контура (на ёмкости или индуктивности) могут достигать опасного для жизни значения. Об этом необходимо всегда помнить!