ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ
Пример 1. Методом коллокации найти приближённое решение уравнения:
y²(x) + (1 + x2) y(x) = -1. (22)
С однородными краевыми условиями первого рода:
y(-1) = 0; (23)
y(1) = 0. (24)
Поскольку в данном случае мы имеем дело с однородной краевой задачей (случай A = B = 0), то полагаем j 0(x) º 0 и решение искомое в форме (6) будем выражать только через линейную комбинацию функций: j i(x) (i = 1, 2, …, n).
Из вида ДУ (22) и краевых условий (23), (24) делаем вывод о чётности решения данной дифференциальной задачи. Поэтому в качестве базисных функций (ограничиваясь двумя базисными функциями) выберем полиномы:
j 1(x) = 1 - x2 и j 2(x) = x2(1 - x2)
Поскольку
j¢1(x) = - 2x и j¢2(x) = 2x - 4x3 = 2x(1 - x2);
то легко видеть, что для данных базисных функций выполняются однородные краевые условия:
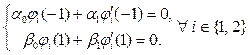
В соответствии с методом коллокации решение y(x) задачи (22) - (24) ищем в виде линейной комбинации функций j1(x) = 1 - x2 и j 2(x) = x2(1 - x2):
y2(x) = c1(1 - x2) + c2x2(1 - x2) (25)
Для подбора двух коэффициентов c1 и c2 на отрезке [-1, 1] выберем две точки коллокации: x0 = 0 и x1 = 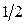 .
.
Далее по формуле (8) составляем невязку:
R(x, ci) º L[y2(x)] - f (x) = 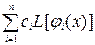 - f (x), (i = 1, 2)
- f (x), (i = 1, 2)
Которая уравнения (22) имеет вид:
R(x, ci) = (c1(1 - x2) + c2x2(1 - x2))² + (1 + x2)×(c 1(1 - x2) + c2x2(1 - x2) ) + 1 =
= – 2c1 + c2(2 - 12x2) + (1 + x2)[c1(1 - x2) + c 2(x2 - x4) ] + 1 Þ
R(x, ci) = 1 – c1(1 + x4) + c 2( 2 – 11x2 - x6 ) (26)
Последовательно подставляя в выражение (26) значения x0 = 0 и x1 = 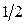 , получим систему уравнений:
, получим систему уравнений:
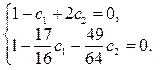 (27)
(27)
Решая систему (27) находим c1 = 0.957; c2 = – 0.022; следовательно, окончательно получаем следующее приближённое решение краевой задачи (22) – (24):
y2(x) » 0.957(1 - x2) – 0.022x2(1 - x2).
Ответ: y2(x) » 0.957(1 - x2) – 0.022x2(1 - x2).
Пример 2. Методом коллокации найти приближённое аналитическое решение краевой задачи:
x4y¢¢ (x)+ x6y¢ (x) - x5y (x) = 6 - 3x3, x Î[1, 2]
с краевыми условиями:
y(1) = 1 и 3y(2) + y¢(2) = 0.5
Поскольку для рассматриваемой краевой задачи решение ищется на промежутке x Î[1, 2] и следовательно x ¹ 0, то рассматриваемое дифференциальное уравнение целесообразно сначала преобразовать к стандартному виду (1):
| y¢¢ (x)+ x2y¢ (x) - x y(x) = (6 - 3x3)/x4 y(1) = 1 и 3y (2) + y¢ (2) = 0.5 | (28) |
Применительно к исходной краевой задаче (1) - (3):
y¢¢ (x)+ p(x)y¢ (x) + q(x) y(x) = f (x), x Î [a, b], (1)
l a [y] º a0 y(a) + a1 y¢ (a)= A, (2)
l b [y] º b0 y(b) + b1 y¢ (b)= B. (3)
задача (28) характеризуется следующими значениями параметров:
| p(x) = x2; q(x) = -x; f (x) = 6/x4 - 3/x; | |
| a = 1; a0 = 1; a1 = 0; A = 1. | b = 2; b0 = 3; b1= 1; B = 0.5 |
Для применения метода коллокации сначала выберем базовые функции
j 0(x) и j i(x), i = 1,2, …, n .
Функцию j 0(x) выберем в виде выражения (14): j 0(x) = d + gx; и далее на основе системы (15):
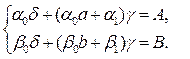 или в нашем случае:
или в нашем случае: 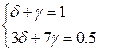
определяем коэффициенты d = 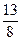 g = -
g = - 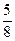 ; Þ j 0(x) = d + gx =
; Þ j 0(x) = d + gx = 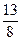 -
- 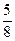 x;
x;
Далее необходимо выбрать подходящие базисные функции j i(x), i = 1,2, …, n. В данном методе количество базисных функций совпадает с количеством узлов коллокации.
При рассмотрении данного примера ограничимся одной базисной функцией
j 1(x) вида (16): j i(x) = gi(x - a)i + (x - a) i+1, или при i = 1, j 1(x) = g1(x - 1) + (x - 1)2 для которой коэффициент g1 определяем из соотношения (19):

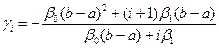 или в данном случае
или в данном случае 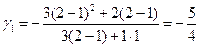 ,
,
Таким образом, мы получили базисную функцию: j 1(x) = (x - 1)2 - 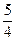 (x - 1).
(x - 1).
Возьмём в качестве узла коллокации середину рассматриваемого промежутка [1, 2], т.е. точку x1 = 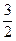 и потребуем, чтобы функция y 1(x) = j 0(x) + c1j 1(x) удовлетворяла в этой точке заданному дифференциальному уравнению (28):
и потребуем, чтобы функция y 1(x) = j 0(x) + c1j 1(x) удовлетворяла в этой точке заданному дифференциальному уравнению (28):
y¢¢ (x)+ x2y¢ (x) - x y(x) = (6 - 3x3)/x4
подставим в него все необходимые значения:
j 0(x) = 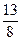 -
- 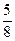 x; j 1(x) = (x - 1)2 -
x; j 1(x) = (x - 1)2 - 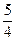 (x - 1); Þ
(x - 1); Þ
y 1(x) = j 0(x) + c1j 1(x) = 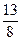 -
- 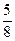 x + c1[(x - 1)2 -
x + c1[(x - 1)2 - 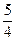 (x - 1)] Þ
(x - 1)] Þ
y 1(x) = 1 - 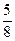 (x - 1) + c1 (x - 1)(x -
(x - 1) + c1 (x - 1)(x - 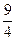 ) Þ при x1 =
) Þ при x1 = 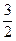 имеем: y 1
имеем: y 1 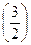 =
= 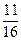 -
- 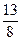 c1;
c1;
y¢1(x) = - 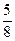 + c1[ 2(x - 1) -
+ c1[ 2(x - 1) - 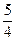 ] Þ при x1 =
] Þ при x1 = 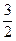 имеем: y¢1
имеем: y¢1 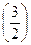 = -
= - 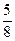 -
- 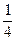 c1;
c1;
y¢¢1(x) = 2 c1;
В результате подстановки указанных величин в уравнение (28) получим:
2 c1 + 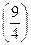
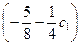 -
- 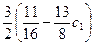 =
= 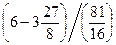 ,
,
решая это уравнение относительно c1 получаем, что c1 = 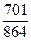 .
.
Таким образом, простейшая коллокация с одним узлом приводит к приближению решения данной краевой задачи (28) квадратичной функцией:
y1(x) = 1 - 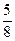 (x - 1) +
(x - 1) + 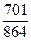 (x - 1)(x -
(x - 1)(x - 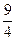 ).
).
Точное решение данной краевой задачи равно: y (x) = 1/x2.
Замечание. Согласно идее метода коллокации приближённое решение yn(x) (6):
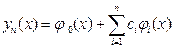
в точках коллокации xiÎ (a, b) должно удовлетворять данному дифференциальному уравнению (1). И, следовательно, в этих точках оно должно было бы совпадать с точным решением y(x) данной краевой задачи (1) - (3). Однако это не так, в чём легко убедиться, сравнивая полученное в примере 2 приближённое решение y 1(x) в узле коллокации x1 = 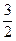 , равное y 1
, равное y 1 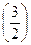 » 0.38 с известным (из других источников) точным значением решения y
» 0.38 с известным (из других источников) точным значением решения y 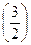 = 0.4(4).
= 0.4(4).
§3. Метод Галёркина.
Рассмотрим линейную краевую задачу для ОДУ второго порядка, определяемую соотношениями (1) - (3).
L [y] º y¢¢ (x)+ p(x)y¢ (x) + q(x) y(x) = f (x), x Î [a, b], (1)
l a [y] º a0 y(a) + a1 y¢ (a)= A, (2)
l b [y] º b0 y(b) + b1 y¢ (b)= B. (3)
Через yn(x) будем обозначать приближённое аналитическое значение точного решения y(x) краевой задачи (1) – (3), которое необходимо получить.
Пусть на отрезке [a, b] задана система базисных функций, интегрируемых с квадратом:
u0(x), u1(x), u2(x), …, un(x), …, (29)
удовлетворяющая следующим условиям:
1. Система (29) является ортогональной системой функций, если две любые функции этой системы взаимно ортогональны на [a, b], т.е. их скалярное произведение* удовлетворяет следующему условию:
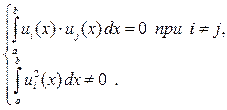 (30)
(30)
(*основные определения аксиоматики скалярного произведения функций приведены в приложении к данной лекции).
2. Система (29) является полной ортогональной системой функций, т.е. не существует никакой другой отличной от нуля функции, ортогональной ко всем функциям ui(x) (i = 0, 1, 2, …).
3. Из полной ортогональной системой функций (29) можно выбрать конечную подсистему базисных функций ui(x) (i = 0, 1, 2, …, n) так, чтобы функция u0(x) удовлетворяла неоднородным краевым условиям:
| la [u0(a)] º a0 u0(a) + a1 u0¢(a)= A, lb [u0(b)] º b0 u0(b) + b1 u0¢(b)= B. | (31) |
а функции ui(x) (i = 1, 2, …, n ) удовлетворяли бы однородным краевым
условиям:
| la [ui(a)] º a0 ui(a) + a1 ui¢(a)= 0, lb [ui(b)] º b0 ui(b) + b1 ui¢(b)= 0. (i = 1, 2, …, n ) | (32) |
Приближённое решение yn(x) краевой задачи (1) – (3) как обычно ищется в
виде линейной комбинации.
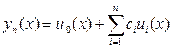 (33)
(33)
Поскольку рассматриваемая дифференциальная краевая задача (1) – (3) является линейной, то из (31), (32) следует, что функция yn(x), определяемая условием (33), удовлетворяет краевым условиям (2), (3) при любом выборе коэффициентов сi, т.е. при указанных выше требованиях к функциям ui(x) (i = 1,2, …, n), u0(x) определяемое выражением (33) приближённое решение yn(x) гарантированно удовлетворяет краевым условиям (2), (3) при любых значениях коэффициентов ci.
Покажем это, например, для точки x = a.
Действительноиз (33) следует, что:
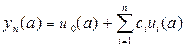 и
и 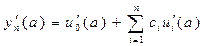 ,
,
далее, учитывая, что в соответствии с (31), (32):
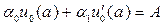 и
и 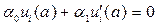 , (i = 1,2, …, n).
, (i = 1,2, …, n).
из краевого условия (2) в силу его линейности при x = a имеем:
la [yn(x)] = a0yn(a) + a1y¢n(a) =
= a0u0(a) + a1u¢0(a) + 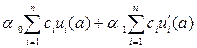 =
= 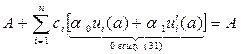 .
.
Аналогично можно показать, что при x = b выполняется условие:
b0yn(b) + b1y¢n(b)= B.
Таким образом, мы показали, что, определяемая выражением (33) и удовлетворяющая требованиями (31), (32) функция yn(x) гарантированно удовлетворяет краевым условиям (2), (3) при любых значениях коэффициентов ci.
При подстановке в ДУ (1) вместо y(x) приближённого решения yn(x) получим:
L[yn(x)] - f (x) = L[u 0(x)] - f (x) + 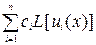 º R(x, c1, c2, ...,cn), (i = 1,2, …, n) (34)
º R(x, c1, c2, ...,cn), (i = 1,2, …, n) (34)
где R(x, c1, c2, ...,cn) невязка, обусловленная отличием точного и приближённого решений. Очевидно, что при подстановке в выражение (34) вместо приближенного решения yn(x) точного решения y(x) рассматриваемой краевой задачи функция невязки будет тождественно равна нулю:
R(x, c1, c2, ..., cn) º 0 при a £ x £ b.
Поэтому для получения приближённого решения yn(x), близкого к точному решению y(x), нужно подобрать коэффициенты сi (i = 1, 2, … ,n) так, чтобы функция
R(x, c1, c2, ..., cn) была «в каком-то смысле» мала.
Обычно коэффициенты сi (i = 1, 2, … ,n) выбирают таким образом, чтобы значение интеграла от квадрата невязки
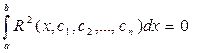 (35)
(35)
было минимальным.
В теории метода Галёркина доказывается, что обеспечить указанную минимальность невязки в среднем можно потребовав, чтобы невязка (34) была ортогональна к базисным функциям ui(x) (i = 1, 2, …, n). Однако при таком подходе к поиску приближённого решения ответить на вопрос, насколько это приближённое решение будет близко к точному решению в общем случае нельзя.
Таким образом, далее, для определения коэффициентов сi (i = 1, 2, … ,n) необходимо записать условие ортогональности невязки:
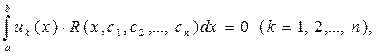
или с учётом (34):
L[u 0(x)] - f (x) + 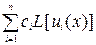 º R(x, c1, c2, ...,cn), (i = 1,2, …, n).
º R(x, c1, c2, ...,cn), (i = 1,2, …, n).
запишем условия ортогональности невязки в более подробной записи:
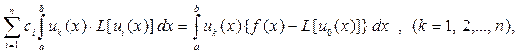
или
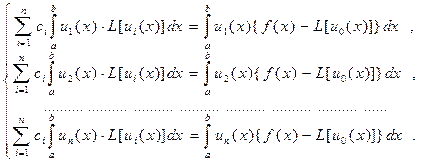 (36)
(36)
Таким образом, получена система линейных алгебраических уравнений относительно коэффициентов сi (i = 1, 2, … ,n).
Замечание. Отметим, что в методе Галёркина при выборе базисных функций требование (30) ортогональности самих базисных функций не является обязательным, если коэффициенты сi (i = 1, 2, …, n) подбирать из условия минимальности интеграла (35). Так, например, взяв за основу полную систему функций, ортогональных на отрезке [a, b], можно выбрать в качестве базисных функций линейные комбинации функций из этой системы. Достаточно лишь, чтобы выбранные функции были линейно независимы на отрезке [a, b].
ПРИМЕР 3Методом Галёркина найти приближённое решение уравнения:
y²(x) + y(x) + x = 0. (37)
С однородными краевыми условиями первого рода:
y(0) = 0; (38)
y(1) = 0. (39)
В качестве базисных функций ui(x) выберем следующие функции:
u0(x) º 0, u1(x) = x (1 – x), u2(x) = x2(1 – x),
Данные функции линейно независимы и удовлетворяют нулевым краевым условиям нашей задачи. Приближённое решение задачи ищем в виде:
y2(x) = с1x (1 – x) + с2x2(1 – x) = x (1 – x)(с1 + с2x).
Подставляя y2(x) в левую часть уравнения (37) получаем невязку:
R(x, c1, c2) = – 2с1 + с2(2 – 6x) + x (1 – x)(с1 + с2x) + x
Записывая требование ортогональности функции R(x, c1, c2) к функциям u1(x) и u2(x), получим систему уравнений:
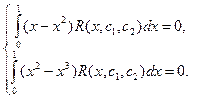
Подставив в эту систему значения R(x, c1, c2) и вычислив интегралы, получим систему линейных алгебраических уравнений для определения коэффициентов c1 и c2 :
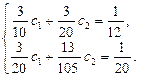
Решая эту систему, получим: 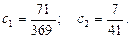
Таким образом, приближённое аналитическое решение данной краевой задачи имеет вид: y2(x) = 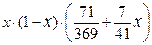
Для оценки качества полученных результатов в таблице 1 в точках отрезка
[0, 1] приведены значения точного решения y(x) данной краевой задачи и приближённого решения y2(x), полученного по методу Галёркина.
Таблица 1 – значения точного и приближённого решения
| xi | 0.25 | 0.50 | 0.75 |
| y2(xi) | 0.044 | 0.069 | 0.060 |
| y(xi) | 0.044 | 0.70 | 0.060 |
Замечание.
Рассмотренные примеры показывают, что при соответствующем выборе базисных функций оказывается возможным найти приближённое решение краевой задачи в аналитической форме.
Если функции p(x), q(x), f (x) в уравнении (1) являются достаточно сложными, то вычисление коэффициентов системы (36) становится слишком громоздким. В таких случаях рекомендуется использовать либо метод коллокации, либо разностный метод.
Заключение (план - аннотация лекции №26).
В лекции 26 рассмотрены метод коллокации и метод Галёркина, позволяющие найти приближённое решение краевой задачи в виде некоторого аналитического выражения.
В методе коллокации (который также иногда называется интерполяционным методом) приближённое решение краевой задачи строится в виде линейной комбинации так называемых базисных функций, причём коэффициенты такой линейной комбинации выбираются из условия совпадения (на некоторой внутренней сетке) искомого приближённого решения с точным решением дифференциальной задачи.
Реализация такого подхода приводит к необходимости решения системы линейных алгебраических уравнений для определения значений коэффициентов в конструкции (в линейной комбинации базисных функций), определяющей вид искомого приближённого решения. Даны рекомендации по выбору базисных функций, используемых для конструирования приближённого решения. Рассмотрен пример решения дифференциальной краевой задачи методом коллокации.
Дано элементарное изложение метода Галёркина (без экскурса в соответствующие разделы функционального анализа для его теоретического обоснования).
Как и в методе коллокации в методе Галёркина приближённое решение также ищется виде линейной комбинации базисных функций, коэффициенты которой выбираются из условия минимизации невязки, обусловленной заменой точного решения дифференциальной задачи искомым приближённым решением. В теории метода Галёркина доказывается, что обеспечить указанную минимальность невязки в среднем можно потребовав, чтобы невязка была ортогональна к базисным функциям, используемым при конструировании приближённого решения.
Реализация такого подхода приводит к необходимости решения системы линейных алгебраических уравнений для определения значений коэффициентов в конструкции (в линейной комбинации базисных функций), определяющей вид искомого приближённого решения. Рассмотрен пример решения дифференциальной краевой задачи методом Галёркина.
Литература:
1. В.М. Вержбицкий. Основы численных методов. – М.: Высшая школа, 2002. – 840 стр.
2. Б.П. Демидович, И.А. Марон, Э.З. Шувалова. Численные методы анализа.
– М.: Наука, 1967. – 368 с.
3. Н.В. Копчёнова, И.А. Марон. Вычислительная математика в примерах и задачах. – М.: Наука, 1972. – 368 с.
Дата добавления: 2015-09-14; просмотров: 9992;
