Критерий Вилкоксона-Манна-Уитни

Данный критерий оперирует не с абсолютными значениями элементов двух выборок, а с результатами их парных сравнений. Например, существенно, что учащийся Петров решил больше задач, чем учащийся Иванов, а на сколько больше – не важно.

Возьмем две выборки³: {x_i}_i = 1…N и {y_j}_j=1…M и для каждого элемента первой⁴ выборки x_i, i = 1…N, определим число a_i элементов второй выборки, которые превосходят его по своему значению (то есть число таких y_j, что y_j > x_i), а также число b_i элементов второй выборки, которые по своему значению равны ему (то есть число таких y_j, что y_j = x_i). Сумма

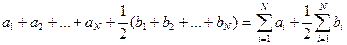
по всем N членам первой выборки называется эмпирическим значением критерия Манна-Уитни и обозначается U.

Алгоритм определения достоверности совпадений и различий для экспериментальных данных, измеренных в шкале отношений, с помощью критерия Вилкоксона-Манна-Уитни заключается в следующем:

1. Вычислить для сравниваемых выборок Wэмп – эмпирическое значение критерия Вилкоксона по формуле (4).

2. Сравнить это значение с критическим значением W_0.05 = 1,96: если Wэмп ≤ 1,96, то сделать вывод: "характеристики сравниваемых выборок совпадают с уровнем значимости 0,05"; если Wэмп > 1,96, то сделать вывод "достоверность различий характеристик сравниваемых выборок составляет 95%".

(4) Wэмп =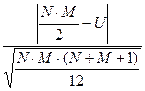

³Ограничение на использование критерия Вилкоксона-Манна-Уитни следующее: каждая выборка должна содержать не менее трех элементов, если же в одной из выборок всего два элемента, то во второй их должно быть не менее пяти.

⁴ Какую выборку считать первой, а какую второй, не имеет значения, хотя при вычислениях удобнее первой считать ту выборку, в которой меньше членов

Математические основы, используемые в ЭС.

Некоторые математические условные обозначения:

" - всеобщность.

$ - существование.

@ - конгруэнтность (равные фигуры).

Þ - .следует

® - стремится к.

Û - эквивалентно.

АÇВ - множества А и В имеют общую часть, пересекаются.

АÈВ - объединение множеств А и В.

АÌВ - А является подмножеством множества В.

хÎА - х принадлежит множеству А.

хÏА - х не принадлежит множеству А.

А = {а, в, с} – множество состоит из элементов.

]а, в[ - интервал (открытый промежуток).

[АВ] - отрезок.

│АВ│ - длина отрезка.

О - пустое множество.

Основные логические связки:

А&В - А и В (АÙВ - коньюнкция).

АÚВ - А или В (дизьюнкция).

┐А - .отрицание (не А).

АÉВ - если А то В (импликация).

АÅВ - либо А либо В (исключающее или).

АºВ - А если и только если В.

События

Н - событие, когда гипотеза верна.

Е - событие, которое подтверждает или не подтверждает гипотезу.

Вероятности

Р(Н) - вероятность, что событие Н истинно.

Р(Е) - вероятность, что событие Е произошло.

Р(┐Н) - вероятность, что событие Н ложно (=1-Р(Н)).

Е₁ и Е₂ - независимы, если и только если Р(Е₁ Ù Е₂)=Р(Е₁)*Р(Е₂).

Р(Н:Е) - условная вероятность наступления Н при наступлении события Е.

Если события Н и Е независимы, то Р(Н:Е)=Р(Н). В общем случае Р(Н:Е)=Р(НÙЕ)/Р(Е). Аналогично Р(Е:Н)=Р(ЕÙН)/Р(Н), поэтому Р(Н:Е)=Р(Е:Н)*Р(Н)/Р(Е).

Теорема Байеса

Р(Н:Е)=Р(Е:Н)_*Р(Н)/(Р(Е:Н)_*Р(Н)+Р(Е:┐Н)_*P(┐Н))

Нахождение Р(Н:Е) не всегда очевидна. Вероятность Р(Е:Н) часто более очевидна и теорема Байеса позволяет рассчитать значение Р(Н:Е) после появления нового события в результате эксперимента или диалога.

Априорные и апостериорные вероятности

Р(Н) - априорная вероятность истинности гипотезы Н без учета факта существования Е.

Р(Н:Е) - апостериорная вероятность гипотезы Н при осуществлении события Е.

Пример расчета: 1. Р(Н) – априорная вероятность гипотезы (или события) Н. 2. При осуществлении события Е₁ запишется значение Р(Е₁:Н). 3. С учетом теоремы Байеса проводится расчет Р(Н:Е₁), т.е. вычисляется апостериорная вероятность Н. 4. Для рассмотрения Е₂ проводится расчет по п.1 приняв значение Р(Н:Е₁) равной Р(Н).

Шансы

Шансы в пользу наступления какого-то события можно вычислить, зная вероятность этого события: О(Е)=Р(Е)/(1-Р(Е)).

Аппроксимации

Р(АÙВ)=min(Р(А), Р(В)), Р(АÚВ)=max(Р(А), Р(В)). Эти выражения верны только при независимости Р и А.

Комбинаторика

Если имеется n событий и из них выбрано х, то число вариантов выбора равно: n!/(n-x)!*x!. Например 4!= 4*3*2*1=24.

Описательная статистика

Среднее, стандартное отклонение и т.д.

Распределения

Нормальное распределение и т.д.

Дискретные и непрерывные переменные

Дискретные – например, да/нет.

Поверхности

Плоские и т.д.

Проблема разделения

Проблема классификации объектов.

Обучающие алгоритмы

Параллельные и последовательные процедуры

Минимальные и максимальные значения

Стратегии поиска решений

Промежуточные выводы

Система комментирующая действия

Линейная интерполяция откликов

Формат данных

Структура ЭС по аналитической химии и метрологии

1. Справочник констант; явлений и свойств; справочник результатов эксперимента (спектров, анализов и др.); веществ, стандартных образцов и реактивов, ГОСТов.

2. Расчеты по математическим моделям для учебных, научных, производственных целей.

3. Методы, методики исследований.

4. Обработка и планирование эксперимента.

5. Теоретические данные (лекции, тесты, задачи). Химия - равновесия, кинетика, термодинамика, механизмы реакций; Физика; Математика; Аналитическая химия; Метрология.

6. Новая информация.

.