Признаки сходимости рядов с положительными членами

Теорема 1 (признак Даламбера).

Дан ряд с положительными членами

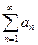(1)

Если существует конечный предел

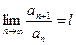. (2)

Тогда:

1) при 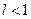ряд (1) сходится;

2) при 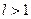ряд (1) расходится.

Доказательство. Воспользуемся определением предела последовательности. Рассмотрим случай, когда 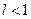, выберем произвольное число 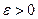так, чтобы число .

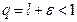Из определения предела последовательности следует, что начиная с некоторого номера 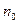, для всех 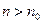выполняется неравенство

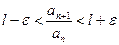(3)

Воспользуемся неравенством 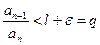. тогда

…………………………..

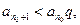
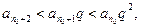
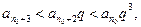
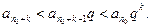
Ряд 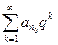при 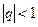сходится, то сходится ряд 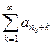, являющийся остатком ряда (1), а следовательно, сходится ряд (1).

2). Рассмотрим случай, когда ,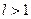

Тогда из неравенства (3) следует, что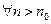

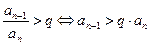
Следовательно, начиная с номера 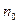не выполняется необходимое условие сходимости ряда, значит в этом случае ряд (1) расходится.

Пример. Исследовать сходимость ряда .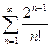

Воспользуемся признаком Даламбера. Найдем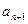

.

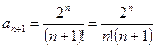Далее находим предел

.

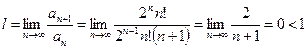Из полученного результата делаем вывод, что исследуемый ряд сходится.

Терема 2 (признак Коши). Пусть для ряда (1) с положительными членами существует предел

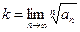(4)

Тогда

1) если 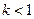, то ряд (1) сходится;

2) Если 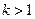, то ряд расходится.

Воспользуемся определением предела последовательности.

Рассмотрим случай, когда 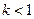. Выберем произвольное, достаточно малое число 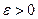, так чтобы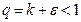

Тогда из равенства (4) следует, что существует такой номер 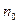, что для всех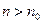

Будет выполняться неравенство

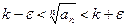(5)

Из неравенства (5) следует, что для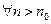

.

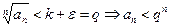Из сходимости ряда 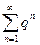и признака сравнения ряд (1) в этом случае сходится.

2) Пусть .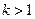

Тогда, обозначив 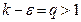, из определения предела получаем, что для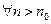

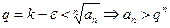. Тогда из расходимости ряда 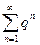( 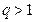) и признака сравнения следует расходимость ряда (1).