Коэффициенты диффузии

В выражениях для диффузионных газовых потоков ко­эффициенты молекулярной и турбулентной диффузии являются единственными параметрами, учитывающими свойства среды. Ес­тественно, что эти величины имеют сложный характер, и их опре­деление - одна из важных задач теории диффузионных процессов.

Коэффициенты молекулярной диффузии. Для газов со сходны­ми молекулами (имеющими почти равные массы и эффективные сечения) Максвелл получил следующее выражение для коэффици­ента молекулярной диффузии:

,

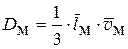где - длина свободного пробега молекул; v_м - скорость их теп­лового движения; черта означает среднее значение величины. При нормальных условиях имеет порядок 10^-5см, v_м = 10^-4 ÷10^-5 см/с.

В силу статистической однородности молекулярного движения величины и 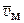, а, следовательно, и коэффициент молекулярной диффузии не зависят от направления. Коэффициент молекулярной диффузии слабо зависит от содержания диффундирующего газа. С увеличением температуры он возрастает пропорционально Т^1+a, где Т - абсолютная температура среды, а - коэффициент, изменяю­щийся от 0,5 до 1. С увеличением давления коэффициент уменьша­ется в обратно пропорциональной зависимости.

Выше отмечалось, что в шахтных условиях молекулярная диф­фузия имеет подчиненное значение в процессе переноса газов. Кроме того, изменения содержания газов, температуры и давления воздуха в активно вентилируемых горных выработках относитель­но невелики. Поэтому при решении задач газопереноса в шахтах можно принимать D_м = const.

Следует иметь в виду, что коэффициент молекулярной диффу­зии газа в среду равен коэффициенту молекулярной диффузии сре­ды в этот газ. Средние значения коэффициентов молекулярной диффузии некоторых газов приведены ниже.

Газ Температура, °С Коэффициент диффузии, см²/с

Аммиак в воздухе 0 0,217

Водород в воздухе - 0,634

Метан в воздухе - 0,196

Оксид углерода в воздухе - 0,129-0,138

Углекислый газ в воздухе 0 0,142

Коэффициенты турбулентной диффузии. В теории турбулент­ности коэффициент турбулентной (или вихревой) диффузии вво­дится как некоторый коэффициент пропорциональности. При этом для его выражения используют три принципиально различных подхода.

В первом способекоэффициент турбулентной диффузии определяют, следуя Буссинеску, как коэффициент пропорционально­сти между потоком газа и градиентом содержания в соответствии с формулой (6.11) - j_т = - D_т·grad c.

Известно, что произведение вектора, каким является в формуле (6.11) градиент содержания, на некоторую величину [в выражении (6.11) ею является коэффициент турбулентной диффузии D_т] может дать вектор [в формуле (6.11) это вектор потока газа] лишь в случае, если эта величина является скаляром или тензором. Коэффициент турбулентной диффузии не может быть скаляром в связи с тем, что в случае равенства производных от содержания по направлениям компоненты газовых потоков по этим направлениям также были бы равны, что в условиях существенно неоднородного и неизотропного турбулентного воздушного потока в выработках невозможно вслед­ствие различия компонент пульсационных скоростей.

Таким образом, остается предположить, что коэффициент турбулентной диффузии в горной выработке — тензор. Можно пока­зать, что в условиях неоднородной и неизотропной турбулентности коэффициент турбулентной диффузии - тензор второго ранга. Тогда компоненты газового потока будут иметь следующее выра­жение:

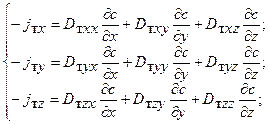(6.17)

Здесь

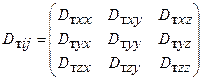(6.18)

(i,j = х,у,z)является тензором коэффициентов турбулентной диф­фузии второго ранга с компонентами D_тxx, D_тxу, ..., D_тzz.

Выражение (6.17) может быть записано в свернутом виде

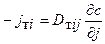. (6.19)

где правая часть представляет собой сумму трех значений 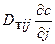, получающихся, если фиксировать i, а j придавать последовательно значения х, у, z (суммирование по двойному индексу).

Выражение (6.19) обычно упрощают, принимая, что оси Ох, Оу, Оz, являются главными осями тензора. Если тензор 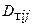симмет­ричный, то 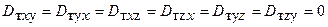и, следовательно, коэффициент турбулентной диффузии определяется только диаго­нальными компонентами D_тxx,D_тyу,D_тzz.

Для однородной и изотропной турбулентности имеет место сферическая симметрия газовых потоков. Следовательно,

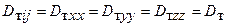. 6.20)

В этом частном случае 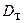может рассматриваться как скаляр.

В выражении (6.11) векторы j_т и gradс коллинеарны*. Следова­тельно, согласно определению, направление вектора gradс являет­ся главным направлением тензора, а ось координат, соответствую­щая ему, - главной осью. Нахождение главных осей тензора коэф­фициентов диффузии для выработки - в ряде случаев задача неоп­ределенная, так как для этого необходимо знать поверхности рав­ных содержаний в потоке, т.е. поле содержаний, что обычно явля­ется конечной задачей исследований. Лишь в простых случаях диффузии главные направления могут быть определены достаточ­но просто. Например, при газовыделении с одной стенки gradс с некоторым приближением можно принять нормальным к этому бо­ку и, следовательно, главные оси тензора будут направлены вдоль потока воздух и перпендикулярно к нему. В более сложных случа­ях главные оси тензора могут иметь и другие направления.

Следует отметить, что принятие тензора D_тy симметричным для случая движения воздуха в горной выработке является также опре­деленным допущением. Для неоднородного и неизотропного турбулентного потока, каким является вентиляционный поток в выра­ботке, тензор коэффициентов турбулентной диффузии будет несимметричным. Ниже отмечается, что компоненты тензора коэф­фициентов турбулентной диффузии могут быть выражены через усредненное произведение (корреляцию) мгновенных значений пульсационной скорости и_niи пути перемешивания для содержа­ния 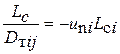(здесь i,j = х, у, z, и_ni = и_п; u_пу =v_n u_nу =w_n). Для симметричного тензора должны соблюдаться равенства 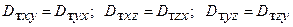, что приводит к соотношениям 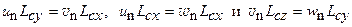. Однако для неизотроп­ных вентиляционных потоков корреляция 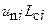несимметрична относительно i и j, а это не отвечает приведенным равенствам. Не­симметричность тензора коэффициентов турбулентной диффузии для шахтных вентиляционных потоков косвенно доказывается фак­тором различной интенсивности турбулентной диффузии в разных направлениях.

Отмеченные приближения, которые применяют при решении практических задач шахтной газовой динамики, в настоящее время не имеют оценки. Применительно к условиям диффузии в призем­ном слое атмосферы погрешности незначительны (в некоторых случаях они составляют 15-20 %). Однако степень анизотропности шахтных вентиляционных потоков значительно выше атмосфер­ных, что может привести к необходимости учета факта несиммет­ричности тензора диффузии.

Второй способопределения коэффициента турбулентной диффузии основан на использовании теории Прандтля о пути перемешивания, согласно которой компоненты потока газа можно определять как сумму трех слагаемых:

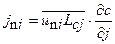. (6.21)

Здесь, подобно тому, как это было принято в выражении (6.19) - 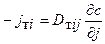, суммирование производится по двойному индексу (j); i = j = х,у,z; 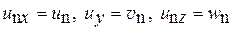; L_c - путь перемешивания для содержа­ния.

Из выражения 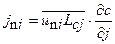следует, что коэффициент турбулентной диффузии является тензором второго ранга

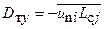(6.22)

определяемым девятью компонентами -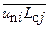

Сопоставляя методы выражения коэффициента турбулентной диффузии по Буссинеску и Прандтлю, видим, что в первом случае коэффициент турбулентной диффузии остается неопределенным, во втором - определяется через характеристики турбулентного движения ( ).

В случае плоского потока ( 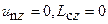) коэффициент турбу­лентной диффузии в поперечном к основному движению направ­лении определяется из выражения (6.21):

,

.

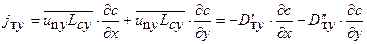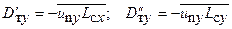В случае изотропной турбулентности можно принять L_cx = L_су, что приводит к равенству

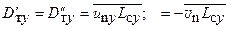, (6.23)

т.е. в этом частном случае коэффициент турбулентной диффузии является скаляром.

Если в уравнении (6.23) v_n выразить по Прандтлю через путь перемешивания для импульса L, то для плоского потока получим вы­ражение

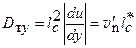, (6.24)

где 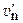среднее квадратичное значение v_п

;

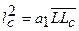а₁ - коэффициент пропорциональности между u_n и v_п. Если принять, что

L / L_с = а₂ = сопst, (6.25)

то

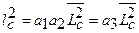. (6.26)

Величина 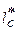для случая диффузии газа является аналогом пути перемешивания для импульса по Карману [21] (не тождественному прандтлевскому пути перемешивания).

Из уравнения 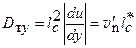видно, что, имея какие-либо гипотезы отно­сительно величин l_С( 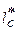), можно, измеряя в потоке, опреде­лить коэффициент турбулентной диффузии. Наиболее простым до­пущением является отождествление l_с путем перемешивания для импульса l; во многих случаях такое приближение дает вполне удовлетворительные результаты.

Следующим шагом в этом направлении является принятие пропорциональности между l_с и l; значение коэффициента пропор­циональности между ними зависит от свойств диффундирующего газа, разности содержаний газа в диффундирующем объеме и в среде. По имеющимся сведениям, этот коэффициент больше 1; для азота он равен ~ 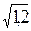, для гелия ~ 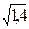. Имеются попытки оце­нить l_с через l и критерий Ричардсона, характеризующий затуха­ние турбулентности под действием объемных (гравитационных) сил при диффузии активного газа.

Наконец, третий способ определения коэффициента турбулент­ной диффузии основан на представлении процесса диффузии как случайного движения жидких частиц, первоначально сконцентри­рованных в некоторой области. Бэтчелор показал, что и в этом слу­чае коэффициент турбулентной диффузии является тензором вто­рого ранга. Запись его (для случая однородной турбулентности), однако, имеет иной вид:

,

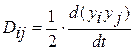где у_i, y_j - лагранжевы координаты жидкой частицы, величины слу­чайные, являющиеся функцией времени.

Представление коэффициента турбулентной диффузии в виде тензора имеет в основном теоретическое значение. В настоящее время практически ничего неизвестно о недиагональных компо­нентах этого тензора. Изученные в какой-либо степени компоненты тензора диффузии — это диагональные компоненты D_тxx,D_тyу,D_тzz, которые в дальнейшем и будут рассматриваться. Для простоты на­писания обозначим D_тxx = D_тхи т.д.

Необходимо отметить, что в общем случае коэффициент турбу­лентной диффузии является функцией координат. Это можно ви­деть, например, из уравнения (6.24), где величины dи/dу, v´_n, l_с для потоков в горных выработках являются функциями поперечных координат [23], а в некоторых случаях (изменение сечения по длине выработки, свободные струи) - и продольной координаты. Эти же величины являются и функциями скорости потока (точнее, числа Рейнольдса - Rе* потока), что говорит о существовании зави­симости коэффициента турбулентной диффузии и от числа Rе.

Данные о коэффициентах турбулентной диффузии в горных вы­работках немногочисленны, что в значительной степени объясня­ется техническими трудностями их измерений. Имеющиеся сведе­ния частично основываются на данных о коэффициенте турбулент­ного обмена для импульса и предположении о пропорциональности ему коэффициента турбулентной диффузии [24].

К.М. Тумаковой были установлены автомодельность попереч­ных составляющих относительного коэффициента турбулентной диффузии:

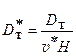
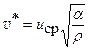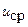; - средняя скорость потока; α – коэффициент аэродинамического сопротивления; r - плотность потока; Н - вы­сота выработки) по числу Рейнольдса, начиная от Rе = 13600, а также равенство вертикальной и горизонтальной поперечных со­ставляющих коэффициента диффузии 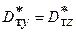. Их значения в яд­ре потока равнялись 0,02, а на расстоянии 0,13H и 0,8H от кровли - 0,03.

В ряде случаев хорошие результаты получаются, если использо­вать средние по высоте (ширине) выработки значения коэффициен­тов турбулентной диффузии.

Коэффициент турбулентной диффузии может быть рассчитан по характеристике рассеивания газа. Для случая однородной и изо­тропной турбулентности в равномерном потоке воздуха (без гради­ента скорости) распределение содержания газа в газовом факеле за источником газовыделения описывается гауссовой кривой ошибок:

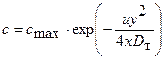, (6.27)

где с - содержание газа в точке с координатами х,у;z - расстояние от источника вниз по потоку; у — расстояние от точки, соответст­вующей максимальному содержанию газа с_mах в плоскости х = соnst, измеряемое в направлении, перпендикулярном направле­нию движения воздуха; и - скорость потока воздуха.

Если в формуле (6.27) с выразить как часть с_mах, то из нее можно определить D_т. Например, полагая с = с_mах/2, получим

D_т= 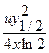, (6.28)

где 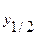- расстояние от оси газового факела до точки в его попе­речном сечении, в которой с = с_mах/2.

Все величины в уравнении (6.27) поддаются прямому измере­нию: и и х измеряют непосредственно на месте эксперимента, 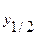- по графику зависимости с(у), построенному на основании измерения содержания на расстоянии от источника, равном х.

Поскольку выражение (6.27) справедливо лишь для однородной и изотропной турбулентности, то в силу равенства (6.20) по нему определяют диагональные члены тензора коэффициентов диффу­зии, не зависящие от координат.

Известно, что турбулентность шахтных вентиляционных пото­ков неизотропна; ее можно считать однородной лишь в направле­нии основного течения (при неизменных форме сечения, шерохо­ватости стен и расходе воздуха). Поэтому для шахтных условий выражение (65.28) дает, во-первых, неточные значения D_ти, во-вторых, лишь некоторые средние значения поперечной компонен­ты тензора D_тy. Погрешности будут возрастать по мере приближения источника газа от оси потока к стенке, так как при этом источ­ник попадает в области все большего градиента скорости, т.е. все большей анизотропии турбулентности.

Учитывая экспериментальное подтверждение аналогии Рейнольдса для процессов переноса импульса и пассивной примеси при те­чениях в пристеночной области, коэффициенты диффузии шахт­ных вентиляционных потоков при диффузии пассивных газов в первом приближении можно принимать равными коэффициенту турбулентного обмена для импульса. Для чисел Рейнольдса от 1,25·10⁴ до 3,72·10⁴ относительные значения последних для штрекообразной выработки прямоугольного сечения, закрепленной рам­ной крепью из круглого леса с продольным калибром 7,5, относи­тельной шероховатостью в направлении вертикальной оси 8,9, го­ризонтальной (перпендикулярной основному движению) 8,4 при­ведены на графиках рис. 6.1 и 6.2, где y - координата, перпендику­лярная бокам выработки, z - кровле и почве. Пересчет относитель­ных значений турбулентного обмена импульса в абсолютные про­изводится по формуле ε = ε*v*D , где D - характерный линейный размер потока (например, диаметр). Приведенные на графиках данные соответствуют средним по сечению абсолютным значениям коэффициентов турбулентного обмена для импульса ε_у и ε_z, порядка 5·10^-3 м²/с при средней скорости воздуха в выработке u_ср =1 м/с, коэффициенте трения α = 15·10^-3 Н·с²/м⁴, плотности воздуха r = = 1,22 кг/м³, диаметре выработки D = 2,5 м.

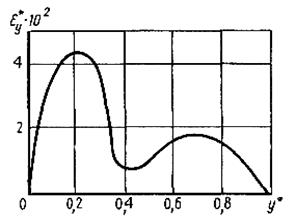
Рис. 6.1. Зависимость от у* = = у/Н (Н - высота выработки)

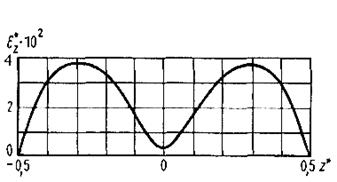
Рис. 6.2. Зависимость от z* = = z/В (В - ши­рина выработки)

Значения компоненты D_тy·10³ (м²/с), полученные для некоторых видов выработок, приведены ниже:

модель штрекообразной выработки, площадь поперечного сечения13,4×14,2 см, средняя скорость воздушной струи 0,25 м/с..........................................1,1

квершлаг, закрепленный анкерами, площадь поперечного сечения 24,5 м²,

скорость воздушной струи 0,5-1,2 м/с........................................................2,4÷4,1

то же, площадь поперечного сечения 23 м², скорость воздушной струи 1,1 м/с........6,8

квершлаг без крепления, сечение сводчатое, площадь поперечного сече­ния 11,8 м², скорость воздушной струи 1,7 м/с.......................................................5,1

то же, площадь поперечного сечения 7,5 м², скорость воздушной струи 0,8 м/с…...1,8

штрек без крепления, сечение сводчатое, площадь поперечного сечения 10 м², скорость воздушной струи 0,27 м/с...............................................................0,8

Для расчета продольных D_тx и поперечных D_тy компонент коэффициента турбулентной диффузии метана в воздухе можно использовать приведенные ниже формулы.

Для штрекообразных выработок

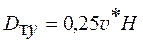; (6.29)

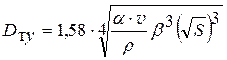, (6.30)

где 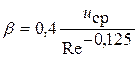, а число Рейнольдса не рассчитывается по .

Для элемента S (м²) поперечного сечения штрекообразной выра­ботки при средней скорости по площади элемента и'_ср (м/с):

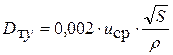. (6.31)

Для круглых гладких и шероховатых труб

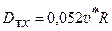, (6.32)

где R - радиус трубы.

Для широкого прямого канала

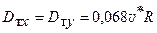. (6.33)

Для диффузии углекислого газа в воздухе

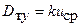, (6.34)

где k: = 3,96·10^-4 м.

В формулах (6.29)-(6.33) использованы следующие обозначения:

Н- высота выработки, м;

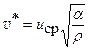- динамическая скорость, м/с;

u_ср - средняя скорость воздушной струи, м/с;

α - коэффициент аэродинамического сопротивления, Н·с²/м⁴;

r -плотность воздуха, кг/м³;

ν - кинематический коэффициент вязко­сти, м²/с;

S - площадь поперечного сечения выработки, м².

По этим формулам для некоторых средних условий (u_ср = 1 м/с; Н= 2,5 м, = 0,1 м/с; R = 1 м) значения компонент D_тx, D_тy состав­ляют порядка 10^-3 м /с.

Коэффициент турбулентной диффузии D характеризует рассеи­вание газа в потоке за счет работы турбулентных пульсаций. В ряде случаев на перемещения диффундирующего газа налагаются более сильные движения, вызываемые наличием сдвига (градиента) ско­рости потока. Именно к таким потокам - "потокам со сдвигом" - относятся шахтные вентиляционные потоки.

В 1951 г. В.Н. Воронин показал, что при движении газового об­лака по выработке его продольная деформация определяется про­филем скоростей. В 1953 г. Дж. Тэйлор опубликовал решение зада­чи продольной турбулентной диффузии примеси от мгновенного источника в круглой трубе. Им было показано, что продольное рас­сеивание примеси, вызываемое градиентом скорости, существенно больше, чем рассеивание, вызываемое турбулентными пульсация­ми скорости. Дж. Тэйлор предложил оценивать суммарный эффект продольного рассеивания примеси относительно плоскости, дви­жущейся со средней скоростью потока, коэффициентом, который получил название эффективного коэффициента диффузии D_Э:

D_Э = D_г = D_тх, (6.35)

где D_г - коэффициент диффузии, вызываемый наличием градиента скорости (коэффициент градиентной диффузии, или коэффициент дисперсии, по Дж.Тэйлору виртуальный, эффективный, действи­тельный коэффициент диффузии); D_тх - коэффициент продольной турбулентной диффузии.

Газовый поток, вызываемый градиентной диффузией, определя­ется выражением

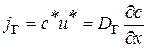, (6.36)

где 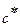, - отклонения соответственно содержания и скорости потока в точке от их средних по поперечному сечению значений;

;

;

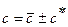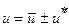с, и - соответственно усредненное по времени содержание и ско­рость потока в точке; 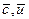- их средние по поперечному сечению значения.

Коэффициент D_э может быть определен в точке или быть усред­ненным.

Исследования С.П. Грекова и А.Е. Калюсского позволили полу­чить следующее выражение для эффективного коэффициента диф­фузии штрекообразной выработки:

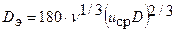; (6.37)

по И.Ф. Ярембашу

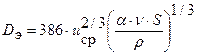. (6.38)

Здесь v - кинематический коэффициент вязкости воздуха, м²/с; u_ср, - средняя скорость воздушного потока, м/с; D - диаметр выра­ботки, м; α - коэффициент аэродинамического сопротивления вы­работки, Н·с²/м⁴; S - площадь поперечного сечения выработки, м²; r - плотность воздуха, кг/м³.

К.Ю. Лайгна и Э.А. Поттер в своих последних работах* дают следующее выражение для среднего по поперечному сечению эф­фективного коэффициента диффузии:

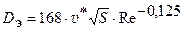, (6.39)

где 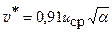, а число Рейнольдса рассчитывают по . Зна­чение D_э можно определить также по графикам, представленным на рис. 6.3.

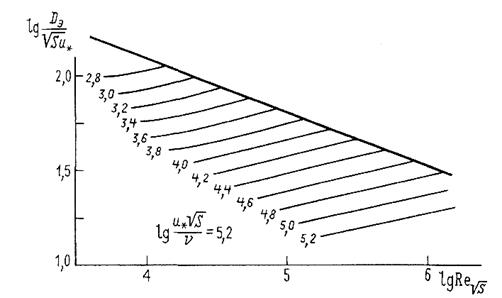
Рис. 6.3. Графики к определению эффективного коэффициента турбулентной диффузии

Расчеты по приведенным формулам и графикам дают значения D_э, порядка нескольких м²/с.

Дж. Тэйлор и К.Ю. Лайгна, исследуя влияние изогнутости кана­ла на коэффициент диффузии, сделали вывод, что этот фактор мо­жет увеличивать D_э до двух раз.

Для изучения газодинамических процессов при действии сво­бодных струй В.Н. Воронин применил коэффициент турбулентной диффузии k_т, определив его как отношение среднего содержания газа в поперечном сечении ядра постоянной массы свободной струи с_як среднему содержанию на ее границе с_гр:

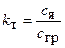. (6.40)

Значения k_т зависят от условий распространения свободной струи и изменяются от 0,3 до 0,9.

Основываясь на подобии полей скоростей и содержаний в ядре постоянной массы свободной струи, В.Н. Воронин получил следующие выражения для коэффициента турбулентной диффузии чистых (не содержащих газа в начальном сечении) свободных струй:

для основного участка круглой струи

k_т = 1÷1,84А; (6.41)

для основного участка плоской струи

k_т = 1÷1,44А´;. (6.42)

В приведенных формулах

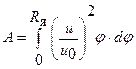(6.43)

, (6.44)

где R_Я - радиус ядра постоянной массы; и - скорость в точке с координатами х, у; и₀ - осевая скорость; φ_я - относительная координата границы ядра постоянной массы;

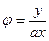; (6.45)

а - коэффициент структуры свободной струи, зависящий от на­чальных турбулентности и профиля скорости (по В.Н. Воронину, для круглой струи а = 0,044÷0,053, для плоской а = 0,09÷0,12).

Значения коэффициентов турбулентной диффузии, рассчитан­ные по приведенным формулам, даны на рис. 6.4.

Приведенные выражения справедливы для свободных струй в неограниченном пространстве. В условиях горных выработок свободные струи часто распространяются в ограниченных объемах, при этом воздухообмен между струей и окружающим воздухом определяется не только структурой струи, но и структурой воздушных потоков в окружающей ее среде, которая в свою очередь зависит от геометрии ограничивающих поверхностей и их шероховатости и в общем случае отлична от таковой в неограниченных объемах. В результате коэффициенты турбулентной диффузии струй в ограниченных пространствах отличаются от таковых в неограни­ченных пространствах. Впервые это было отмечено Ю.М. Первовым, который предложил учитывать его соответствующим измене­нием коэффициента структуры а.

а

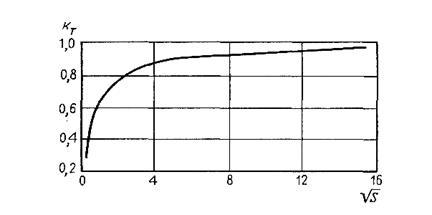
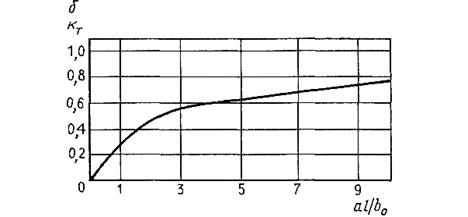
Рис. 6.4. Зависимость k_т от 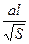для круглой (а) и аl/b₀ для плоской (б) струй (l - длина струи, S - площадь ее начального сечения)

С учетом п - отношения ширины камеры к ширине выработки, подводящей воздух, согласно Ю.М. Первову:

для струи, выходящей из квадратного гладкого отверстия, при

n >2,33а = 0,077(n-0,5)(n + 1).

При п < 2,33 коэффициент струк­туры не зависит от степени ограничения и равняется 0,42;

для струи, выходящей из круглой гладкой трубы, при п > 2,33

а = 0,062 (п -0,5)

При n<2,33 а = 0,034;

для плоской струи при п > 3,12

а = 0,2(n^3/2 - 1,25n + 0,25)/(n^3/2 - 1),

а при п <3,12

а = 0,085 .

Подобное явление было установлено при распростране­нии свободных ветровых струй в карьерах.

По В.Н. Воронину, коэффициент турбулентной диффузии струи, и начальном сечении которой уже имеется некоторое количество газа с содержанием с₀(частично загазованная струя), определяется по формуле

. (6.46)

При этом принимается, что коэффициент турбулентной диффузии не зависит от турбулентной структуры газовоздушной среды вне свободной струи, т.е. газообмен между струей и средой определяется лишь течением в струе, а это, видимо, справедливо только для затопленных струй, распространяющихся в неограни­ченном пространстве. Поскольку через границу свободной струи происходит обмен турбулентными массами, то турбулентная структура струи должна зависеть от структуры движения и энергии привносимых в нее извне масс. При исследованиях затопленных струй, распространяющихся в ограниченных пространствах (карь­еры, тупиковые выработки, камеры и т.п.), была установлена завиисимость их угла раскрытия [а следовательно, в соответствии с формулой (6.36) - и коэффициента структуры струи] от геометрии ограничивающих поверхностей, что должно быть связано с турбулентной структурой вторичных токов, заполняющих пространство между ограничивающими поверхностями и границей свободной струи*.

В общем случае структура вторичных токов должна зависеть от начального расхода воздуха в струе, и для точного описания газообменных процессов, связанных с распространением свободных струй, с помощью коэффициента турбулентной диффузии В.Н. Во­ронина необходимо определить зависимости его от диффузион­ных свойств внешней среды (например, от коэффициента диффузии D_т.

Более строгим является исследование процессов газопереноса в свободных струях на основе ранее рассмотренных коэффициен­тов турбулентной диффузии и эффективных коэффициентов диф­фузии. Исследования для их установления применительно к струй­ным движениям в горных условиях были выполнены К.Ю. Лайгна, Э.А. Поттером и О.А. Суллакатко. Ими впервые получены выра­жения для расчета коэффициентов турбулентной диффузии огра­ниченной (степенной) струи [12], в частности, для эффективных коэффициентов продольной турбулентной диффузии:

круглая турбулентная струя, 30·10³ < Rе < 730·10³:

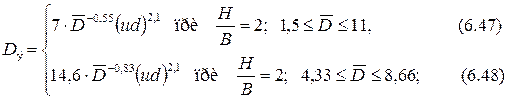
плоская турбулентная струя, 30·10³ < Rе < 730·10:

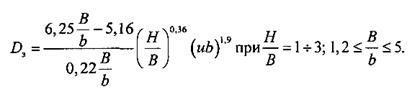(6.49)

Здесь - коэффициент стеснения струи; S - площадь поперечного сечения выработки; d - начальный диаметр струи; и -средняя начальная скорость струи; Н, В - соответственно высота и ширина выработки; b - начальная ширина струи.

ТЕМА №7. ИНТЕГРАЛЬНЫЕ ГАЗОДИНАМИЧЕСКИЕ ЭФФЕКТЫ В ШАХТАХ

Общие положения

Во многих случаях по­лезные результаты могут быть получены более простым инте­гральным методом.

Интегральный метод, или метод усредненных характеристик, ос­нован на том факте, что локальные газодинамические эффекты в ко­нечном итоге выступают в виде некоторых обобщенных, или инте­гральных, усредненных закономерностей, таких, например, как изме­нение среднего по сечению содержания газа на выходе из забоя, уча­стка, шахты, изменение суммарного дебита газа из выработанного пространства в выработку и др. Предметом интегрального метода анализа является исследование газодинамических процессов в шах­тах, описанных в терминах усредненных характеристик. В интеграль­ном методе использованы такие усредненные характеристики процес­са, как средняя скорость движения, среднее содержание и т.п. Усреднение может производиться по одному, двум, трем измерениям, а также во времени*. Использование усредненных характеристик не требует знания их полей, что существенно упрощает аппарат анализа, а также турбулентных характеристик потока, которые в этом методе обычно учитываются эмпирическими константами. Число параметров процесса сокращается. Все это делает интегральный метод достаточно простым и легко приводящим к конкретным результатам.

Однако замена локальных значений характеристик их усреднен­ными значениями не всегда может пройти без заметного снижения достоверности получаемых результатов. В качестве примера можно привести расчет расхода воздуха по среднему содержанию метана для выработок, где имеются слоевые скопления газа: при достаточ­ности полученного расхода в среднем он не всегда может обеспе­чить ликвидацию зон высокого содержания газа в пристеночных областях. В общем, правомерность и погрешность использования ме­тода средних характеристик определяется их различиями, как в точке, так и во всей области движения, причем, чем больше области, где эти различия существенны, тем менее правомерно использование этого метода и тем больше возни­кающая при этом погрешность.

Основным соотношением интегрального метода является соот­ношение между содержанием газа с, объемным расходом газа J и расходом газовоздушной смеси Q* :

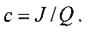(7.1)

Если J и Q взаимонезависимы, изменение содержания прямо пропорционально расходу газа и обратно пропорционально расхо­ду воздуха. В частности, монотонному изменению расхода воздуха в этом случае соответствует монотонное изменение содержания газа.

В ряде случаев расход газа в выработке зависит от расхода воз­духа. При этом возможно появление так называемых переходных газодинамических процессов, при которых обратно пропорцио­нальная зависимость между с и Q нарушается. В общем имеющий практическое значение характер зависимости с(Q) определяется соотношением (7.1) и зависимостью с(J).

Основой метода усредненных характеристик является закон сохранения массы, который применяется к участку выработки конечной длины или к выработке в целом. Для выбранного участка определяют­ся интегральные газовые потоки, поступающие в выработку и вы­ходящие из нее, от всех действующих в выработке источников га­зовыделения. Алгебраическая сумма поступления газа в выработку и его выноса в виде этих потоков за некоторый промежуток време­ни определяет изменение газосодержания в объеме рассматривае­мой выработки за этот же период.

Под интегральным газовым потоком от i-го источника понима­ется количество газа, поступающее в рассматриваемую выработку в единицу времени. Если i-й интегральный газовый поток в выра­ботку объема V обозначить через J_i то, согласно закону сохранения массы и в соответствии с вышесказанным, получим следующее наиболее общее дифференциальное уравнение переноса газа:

(7.2)

или

(7.3)

где п — число интегральных газовых потоков в выработке; ее — из­менение среднего содержания газа в выработке за период времени

В стационарном случае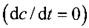

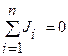(7.4)

Интегральные газовые потоки могут поступать в выработку (вы­ходить из нее) либо со струей воздуха, либо с ее твердых границ.

Интегральный газовый поток, вносимый (выносимый) в выра­ботку вентиляционной струей,

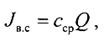(7.5)

где с_ср - среднее содержание газа в поступающем (выходящем) в выработку воздухе; Q - расход воздуха на входе (выходе) в вы­работку.

Интегральные газовые потоки с твердых границ выработки мо­гут иметь различное происхождение и рассчитываться разными способами. Так, интегральный газовый поток с обнаженной по­верхности горных пород

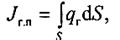(7.6)

где q_г - абсолютное газовыделение с единицы обнаженной поверхности; S - площадь обнаженной поверхности.

Аналогично определяется интегральный газовый поток из гра­ничащего с выработкой выработанного пространства.

Интегральный газовый поток из находящейся в выработке отби­той горной массы может быть определен как произведение абсо­лютного газовыделения q'_г, отнесенного к единице массы отбитой горной породы, на общую отбитую массу М_от:

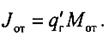(7.7)

Следует иметь в виду, что q_ги q'_г являются функциями времени.