Законы радиоактивного распада

Наблюдения показывают, что радиоактивный распад - явление статистическое: нельзя предсказать, когда именно распадается данное нестабильное ядро, поскольку распад конкретного ядра - случайное событие, имеющее определенную вероятность.

Закон самопроизвольного распада основывается на двух предположениях:

Распад данного атомного ядра не влияет на распад других ядер.

Скорость распада пропорциональна наличному числу N ядер (N>>1).

Таким образом, если в момент t имеется большое число N радиоактивных ядер, то убыль (-dN) числа ядер за время dt пропорциональна N:

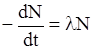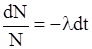или . (10.1)

Величина l, называется постоянной радиоактивного распада. Это основная статистическая характеристика радиоактивного распада данного изотопа, она трактуется как вероятность распада радиоактивного изотопа в единицу времени, зависит от типа радиоактивности, сорта радиоактивного ядра (но не от способа его получения) и не зависит от внешних условий (давления, температуры, числа распавшихся ядер и др.)

Величина А=lN называется активностью нуклида. Она характеризует интенсивность излучения препарата в целом, а не отдельно ядра. Как видно, активность со временем уменьшается пропорционально N.

Согласно (10.1) активность численно равна числу распадов за единицу времени

.

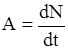Единицей активности в системе СИ является Беккерель (Бк):

1 Бк = 1 распад/с.

В ядерной физике употребляется внесистемная единица активности - Кюри (Ки):

1 Ки = 3,7×10¹⁰ Бк.

Вследствие того, что постоянная распада l не зависит от времени (т.е. от «возраста» ядра), соотношение (2.1) легко интегрируется. Результатом интегрирования и является основной закон радиоактивного распада, имеющий вид:

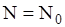е^-lt_, (10.2)

где N₀ - число ядер в произвольно выбранный начальный момент t = 0. Видно, что чем больше l, тем быстрее убывает число N радиоактивных ядер. На рис. 2.1. изображена кривая радиоактивного распада.

Как следует из (10.2) определять время распада всех ядер данного изотопа не имеет смысла (полный распад происходит за t=¥), поэтому

для характеристики интенсивности процесса вводятся следующие величины - период полураспада T_1/2 и среднее время жизни t ядра.

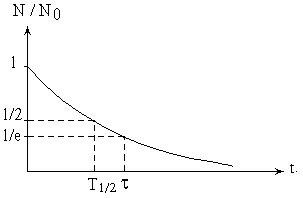
Рис. 2.1.

Период полураспада есть время, за которое число радиоактивных ядер (взятых, конечно, в очень большом количестве), уменьшается вдвое. Согласно (10.2)

,

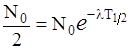откуда

T_1/2=ln2/l . (10.3)

Поскольку для данного нуклида l=const, то и T_1/2=const. Это значит, что какое бы количество радиоактивных атомов данного сорта ни было бы взято, половина из них претерпят распад за одно и то же время.

Среднее время жизни - это время, за которое число радиоактивных атомов уменьшается в е раз (e=2,7...):

,

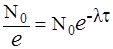откуда t=1/l . (10.4)

Сравнивая (10.3) и (10.4), получим

T_1/2=t ln2.

Периоды полураспадов для известных радиоактивных ядер лежат в очень широких пределах: от 10^-7 с до миллиардов лет.