ДВИЖЕНИЕ МИКРОЧАСТИЦ В СТАЦИОНАРНЫХ ПОЛЯХ

Рассмотрим некоторые простейшие задачи квантовой механики, связанные с решением стационарного уравнения Шредингера для частицы, движущейся в конкретных потенциальных силовых полях. Анализировать полученные решения будем, главным образом, применительно к электрону, поскольку закономерности его движения лежат в основе действия почти всех приборов современной электроники, нашедших применение в технике.

2.5.1. МИКРОЧАСТИЦА В "ПОТЕНЦИАЛЬНОЙ ЯМЕ"

Для описания поведения микрочастицы с помощью уравнения Шредингера необходимо знать зависимость потенциальной энергии частицы от координат, т.е. W_p (x, y, z) . Во многих практически важных случаях силовые поля, воздействующие на частицу, оказываются такими, что зависимость может быть представлена графически в виде «потенциальной ямы» той или иной конфигурации. «Потенциальной ямой» называется ограниченная область силового поля, в которой потенциальная энергия объекта значительно меньше, чем за ее пределами. Например, для электрона в поле сил притяжения к ядру зависимость W_p от x (одномерная «потенциальная яма») – имеет

вид кривой, представленной на рис.2.4, где х - расстояние между электроном и ядром атома.

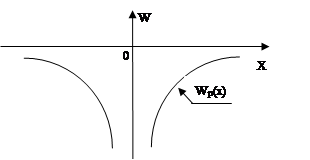Рис. 2.4

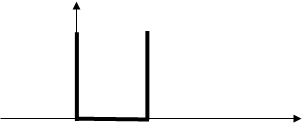
Потенциальная энергия электрона в области такой ямы W_p<0. Однако, решение уравнения Шредингера даже для случая атома водорода является весьма громоздким. Поэтому рассмотрим поведение микрочастицы в одномерной «потенциальной яме» наиболее простой формы – прямоугольной, с бесконечно высокими стенками и плоским дном (рис.2.5). Такую «потенциальную яму» иногда называют «ящиком».

Несмотря на грубость данной модели, она дает возможность выявить многие существенные черты реальных квантово-механических систем, то есть те черты, которые отличают эти объекты от классических. Кроме того, данная модель позволит выявить условия, при которых приемлемы классические представления.

В стационарном поле потенциального «ящика» потенциальная энергия электрона имеет значения:

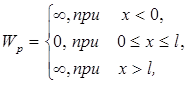(2.32)

где l - ширина «ящика», а энергия отсчитывается от дна “ящика”

до ¥ до ¥

W_p(x)

0 l x

Рис.2.5

В данном случае амплитудное уравнение Шредингера (2.29) можно записать в виде

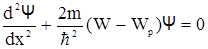. (2.33)

Согласно принятому условию (бесконечно высокие «стенки») частица не может проникнуть за пределы «ящика», поэтому вероятность ее обнаружения, а значит и ψ - функция, за его пределами (в областях X<0 и X>l) равна нулю. На границах «ящика» ( при X=0 и X=l) непрерывная и однозначная волновая функция тоже должна обращаться в нуль:

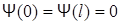. (2.34)

В пределах «ящика» (0 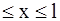) уравнение (2.33) с учетом (2.34) примет вид:

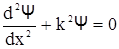, (2.35)

где

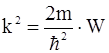. (2.36)

Общее решение дифференциального уравнения (2.35) будем искать в виде

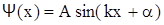, (2.37)

где А и a - произвольные константы.

Используя первое граничное условие (2.34), т.е. ψ (0) = 0, находим, что a =0.

Подставив это значение в (2.37), получим уравнение

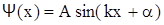, (2.38)

Воспользовавшись вторым граничным условием ψ(l)=0, получим 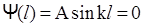, что выполняется не при любом значении параметра k, а лишь в том случае, если

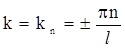,(2.39)

где n =1, 2, 3 , ….

Подставив это значение k в формулу (2.38), найдем волновую функцию микрочастицы

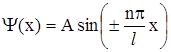. (2.40)

Неизвестная пока величина А может быть найдена из условия нормировки (2.16) ψ - функции:

.

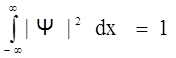Учитывая, что y (x) не обращается в нуль лишь на отрезке 0<x<l, можно записать

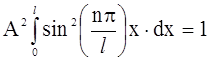. (2.41)

Вычислив интеграл (2.41), получим амплитуду А волновой функции (формула (2.40)) в виде:

А = .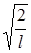

Таким образом, собственные волновые функции микрочастицы в потенциальной "яме" шириной l с бесконечно высокими стенками определяются выражением

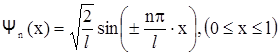. (2.42)

Плотность вероятности нахождения частицы на различных расстояниях от «стенок» ямы равна

.

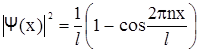Эти результаты представлены графически на рис. 2.6.

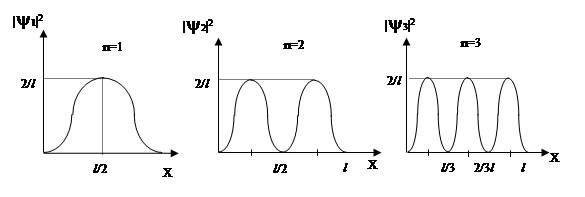Рис.2.6

Интересно отметить, что при любом n в пределах ямы укладывается целое число полуволн де Бройля. Действительно, с учетом формулы де Бройля и соотношения (2.29), получаем

,

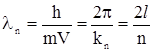откуда следует, что 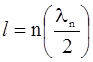, (n=1,2,3...).

Вероятность нахождения микрочастицы неодинакова для разных точек ямы и зависит от числа n. При n = 1 наиболее вероятным местом локализации частицы является середина ямы, а при n=2 вероятность обнаружить частицу в точке х = 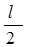равна нулю. Таким образом, нельзя говорить о траектории частицы.

Возможные значения энергии W_n микрочастицы можно найти подстановкой (2.39) в формулу (2.36):

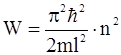, (n=1,2,3...). (2.43)

Итак, поставленная задача полностью решена – найден энергетический спектр (2.43) частицы в яме и соответствующие стационарные функции (2.42).

Анализ соотношения (2.43) показывает, что энергия микрочастицы в потенциальной яме может принимать не любые значения, а лишь набор разрешенных значений - энергетических уровней, соответствующих значениям числа n =1,2,3, …, которое называется главным квантовым числом. Таким образом, энергия микрочастицы в яме квантована, ее энергетический спектр – дискретный (или линейчатый) - рис. 2.7.

Минимальное значение энергии микрочастицы соответствует значению n=1 (основное квантовое состояние):

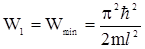. (2.44)

Частица, находясь в яме, не может пребывать в состоянии покоя, поскольку 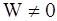. Этот же вывод следует и из соотношения неопределенностей (2.18). Действительно, поскольку неопределенность координаты микрочастицы в яме Dx=l (ширина ямы), а неопределенность импульса 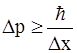, то минимальная кинетическая энергия (соответствует разбросу значений энергии) получается равной

,

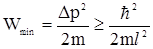что по порядку величины соответствует значению, определяемому формулой (2.44).

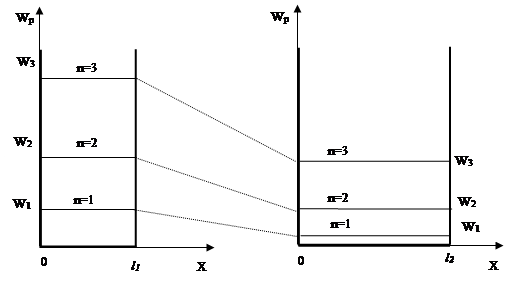а) б)

Рис.2.7

Существование дискретных энергетических уровней энергии доказано здесь лишь для весьма частного и физически нереального случая. Однако, квантованность энергии характерна для всех задач, где движение частицы ограничено конечной областью пространства. Если эта область имеет макроскопические размеры, то уровни энергии будут расположены столь густо, что дискретный спектр оказывается неотличим от сплошного.

Как следует из соотношения (2.43), энергетический интервал между двумя соседними разрешенными энергетическими уровнями равен

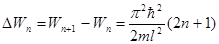, (2.45)

то есть, согласно (2.45) квантование сказывается тем меньше, чем больще l (чем шире потенциальной ящик (рис.2.7)); при l®¥ спектр будет сплошной. Относительный скачок энергии при переходе между соседними уровнями убывает с увеличением квантового числа n:

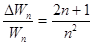. (2.46)

Как следует из (2.46), при больших значениях n (n>>1)

~

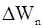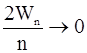
то есть, чем больше n, тем теснее расположены соседние уровни – дискретность спектра становится несущественной. Сделанные выводы подтверждают принцип соответствия квантовых и классических закономерностей в предельных условиях.

Физическая причина квантованности энергии лежит вне рамок квантовой механики. Квантовая механика дает лишь метод правильного отражения реально существующей квантованности с помощью определенного математического аппарата, и в этом ее основное преимущество перед классической механикой.

В случае двухмерного «потенциального ящика» с бесконечно высокими стенками система будет характеризоваться уже двумя квантовыми числами n₁ и n₂ , поэтому

,

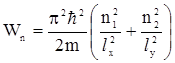где l_х и l_у - размеры ящика по осям Х и U.

Потенциальная яма, подобная рассмотренной, но с W<0, создается, например, для полностью обобществленных электронов внутри металла. Результирующие воздействие на каждый из таких электронов со стороны всех ионов кристалла уравновешивается в среднем воздействием на этот электрон всех остальных электронов, так что потенциальную энергию такого электрона внутри кристалла можно считать равной нулю. На границах тела из-за существования двойного электрического слоя имеет место резкое повышение потенциала и создается потенциальный барьер, ограничивающий яму.