Касательная плоскость и нормаль к поверхности

Пусть в плоскости (х, у, z) имеется область D, в которой задана функция

и = и(х, у, z).

В этом случае говорят, что в области D задано скалярное поле. Если, например, и(х, у, z) обозначает температуру в точке М(х, у, z), то говорят, что задано скалярное поле температур; если область D заполнена жидкостью или газом и и(х, у, z) обозначает давление, то имеется скалярное поле давлений и т.д.

Рассмотрим точки области D, в которых функция и(х, у, z) имеет постоянное значение с:

и(х, у, z) = с.

Совокупность этих точек образует некоторую поверхность. Если возьмем другое значение с, то получим другую поверхность. Эти поверхности называются поверхностями уровня.

Пример 33. Пусть задано скалярное поле .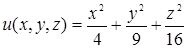

Здесь поверхностями уровня будут поверхности 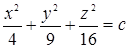, т.е. эллипсоиды с полуосями , , .

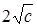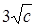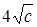Если функция и есть функция двух переменных х и у:

и = и(х, у),

то «поверхностями» уровня будут линии на плоскости Оху:

и(х, у) = с,

которые называются линиями уровня.

Если значения и мы будем откладывать по оси Оz:

z = и(х, у),

то линиями уровня на плоскости Оху будут проекции линий, которые получаются в пересечении поверхности z = и(х, у) с плоскостями z = с. Зная линии уровня, легко исследовать характер поверхности z = и(х, у).

Пример 34. Определить линии уровня функции z = 1 – х² – у².

Линиями уровня будут линии с уравнениями 1 – х² – у² = с. Это окружности с радиусом 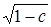. В частности, при с = 0 получается окружность х² + у² = 1.

Касательной плоскостью к поверхности в точке М называется плоскость, содержащая в себе касательные ко всем кривым, проведенным на поверхности через точку М.

Нормалью к поверхности в точке М называется прямая, проходящая через М перпендикулярно касательной плоскости в этой точке.

Если поверхность задана уравнением F(x, y, z) = 0 и в точке М(х₀, у₀, z₀) частные производные 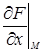, , 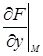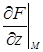конечны и не обращаются в нуль одновременно, то уравнение касательной плоскости к поверхности в точки М(х₀, у₀, z₀) записывается в виде

,

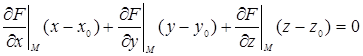а уравнение нормали к поверхности в этой же точке – в виде

.

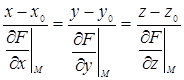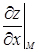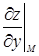Если же уравнение поверхности задано явным образом: z = f(х, у), где частные производные и в точке М(х₀, у₀, z₀) конечны (и могут быть равны нулю одновременно), то уравнение касательной плоскости в точке М записывается в виде

,

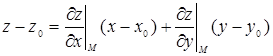а уравнение нормали – в виде

.

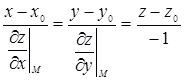Равенство нулю, например 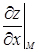, означает, что касательная плоскость параллельна оси Ох, а нормаль лежит в плоскости х = х₀.

Пример 35.Дана поверхность 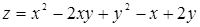. Составить уравнение касательной плоскости и уравнения нормали к поверхности в точке М(1, 1, 1).

Найдем частные производные 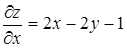и 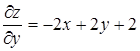и их значения в точке М(1, 1, 1): , .

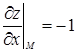Уравнение касательной плоскости:

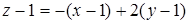, или x – 2y + z = 0.

Уравнение нормали:

(х – 1)/(-1) = (у – 1)/2 = (z – 1)/(-1).

Пример 36. К поверхности х² + 2у² + 3z² = 11 провести касательные плоскости, параллельные плоскости х + у + z = 1.

Здесь F(x, y, z) = х² + 2у² + 3z² – 11. Найдем частные производные: 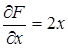, , 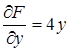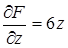. Из условия параллельности касательной плоскости и данной плоскости следует, что (¶F/¶x)/1 = (¶F/¶y)/1 = (¶F/¶z)/1, или (2х)/1 = (4у)/1 = (6z)/1. Присоединив к этим уравнениям уравнение поверхности х² + 2у² + 3z² = 11, найдем координаты точек касания: 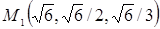и 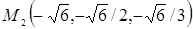. Следовательно, уравнения касательных плоскостей имеют вид

,

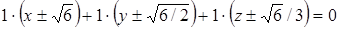т.е.

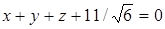и .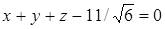

Задание для самостоятельной работы

96. Найти линии уровня функции .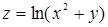

97. Найти линии уровня функции .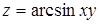

98. Найти линии уровня функции .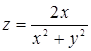

99. Написать уравнение касательной плоскости и нормали к поверхности 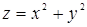в точке M(1; -2; 5).

100. Написать уравнение касательной плоскости и нормали к поверхности 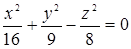в точке M(4; 3; 4).

101. Написать уравнение касательной плоскости и нормали к поверхности 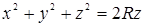в точке M(R cos a; R sin a; R).

102. К поверхности 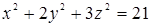провести касательные плоскости, параллельные плоскости .

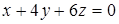103. К эллипсоиду 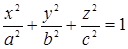провести касательные плоскости, отсекающие на положительных координатных полуосях равные по величине отрезки.

104. К поверхности 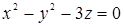провести касательную плоскость, проходящую через точку M(0; 0; -1) , параллельно прямой .

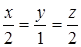105. На поверхности 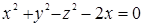найти точки, в которых касательные плоскости параллельны координатным плоскостям.