Рассеивание снарядов и его причины

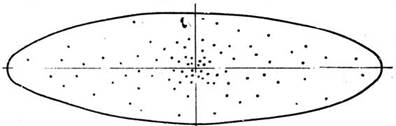
Если произвести большое количество выстрелов из одного и того же орудия в возможно одинаковых условиях (одинаковые заряды и снаряды, одна и та же установка прицельных приспособлений, одинаковые метеорологические условия и т. п.), то каждый снаряд опишет свою траекторию, не совпадающую ни с какой другой траекторией, и упадет в своей точке. Точки падения снарядов расположатся на некоторой площади, называемой площадью рассеивания.

Рассеиванием снарядов называется явление разброса точек падения снарядов при стрельбе из одного и того же орудия в возможно одинаковых условиях.

Совокупность всех траекторий, какие могут быть получены при стрельбе из данного орудия в данных условиях, называется снопом траекторий.

Центр площади рассеивания называется центром рассеивания, а воображаемая траектория, проходящая через центр рассеивания, — средней траекторией.

При небольшом количестве выстрелов распределение точек падения снарядов кажется случайным и сделать какие-либо выводы о закономерностях рассеивания нельзя. Однако если, например, произвести 100—200 выстрелов в возможно одинаковых условиях, то уже нетрудно будет заметить закономерность распределения точек падения. Большим количеством опытов установлено, что рассеивание снарядов подчиняется определенному закону, называемому законом рассеивания.

Рассмотрим свойства закона рассеивания.

Рассеивание не беспредельно. При достаточно большом количестве выстрелов площадь рассеивания приобретает форму геометрической фигуры, называемой эллипсом. При стрельбе из орудий, а также из минометов и боевых машин на малые дальности эллипс вытянут в направлении стрельбы; при стрельбе из минометов и боевых машин на большие дальности эллипс более растянут в стороны. В отдельных случаях площадь рассеивания имеет форму круга (но круг можно рассматривать как частный случай эллипса, у которого полуоси равны). Таким образом, площадь, на которую падают снаряды, ограничена, т. е. имеет предел.

Рассеивание симметрично. Это значит, что точки падения снарядов располагаются в эллипсе так, что впереди центра рассеивания будет столько же воронок, сколько и сзади, вправо от центра рассеивания — столько же, сколько и слева.

Рассеивание неравномерно. В пределах эллипса рассеивания точки падения располагаются гуще у центра рассеивания, а чем дальше от центра, тем точек падения меньше.

Таким образом, закон рассеивания кратко формулируется так: при достаточно большом числе выстрелов, произведенных в возможно одинаковых условиях, рассеивание имеет предел, оно симметрично и неравномерно.

Численным выражением закона рассеивания, отражающим три его основных положения, является шкала рассеивания.

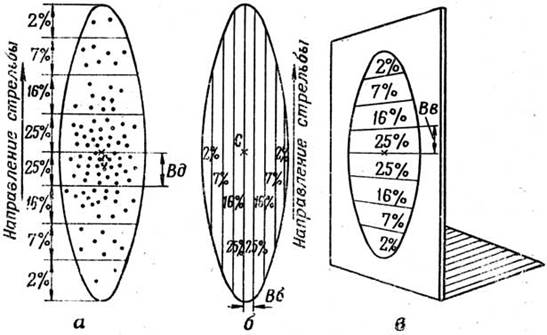
Если эллипс рассеивания разделить пополам (рис.7), а затем каждую половину разделить еще на четыре одинаковые полосы, то при большом количестве выстрелов в каждую из этих полос попадает определенное количество снарядов: в полосы, расположенные непосредственно справа и слева от центра рассеивания, — по 25% снарядов, в соседние с ними полосы — по 16%, в третьи от центра рассеивания полосы — по 7%, в крайние полосы — по 2% снарядов.

Если разделить эллипс рассеивания на восемь равных поперечных полос, получится шкала рассеивания по дальности (рис.7а).

Если разделить эллипс рассеивания на восемь равных продольных полос, получится шкала рассеивания по направлению (рис.7б).

Если пересечь сноп траекторий вертикальной плоскостью, то в сечении получится вертикальный эллипс рассеивания; разделение вертикального эллипса на восемь равных горизонтальных полос дает шкалу рассеивания по высоте (рис.7в).

Рис. 7. Эллипс рассеивания: а — шкала рассеивания по дальности; Вд — срединное отклонение но дальности; б — шкала рассеивания по направлению; Вб — срединное отклонение по направлению; б — шкала рассеивания но высоте; Вв — срединное отклонение по высоте.

Каждая полоса, равная восьмой части всего эллипса, называется срединным отклонением.

Срединные отклонения являются характеристиками закона рассеивания:

· в горизонтальной плоскости — срединное отклонение по дальности— Вд, срединное отклонение по направлению— Вб;

· в вертикальной плоскости — срединное отклонение по вы соте - Вв.

Величины срединных отклонений для каждой системы, снаряда, заряда и дальности указаны в Таблицах стрельбы. В практике пределы рассеивания снарядов обычно принимают равными четырем срединным отклонениям от центра рассеивания по каждому направлению.

Рассеивание снарядов зависит от многих причин, которые можно разбить на три группы: разнообразие начальных скоростей снарядов; разнообразие углов бросания и направлений стрельбы; разнообразие условий полета снарядов после вылета из канала ствола.

Разнообразие начальных скоростей снарядов вызывается различием весов зарядов, химических свойств пороха зарядов; температуры зарядов; плотностей заряжания; весов снарядов; размеров ведущего пояска и положения его на снаряде и др.

Разнообразие углов бросания и направлений стрельбы вызывается различием установок прицела, уровня и угломера; наводки орудия в горизонтальной и вертикальной плоскостях; углов вылета и боковых смещений орудий при выстреле; мертвых ходов механизмов и др.

Разнообразие условий полета снарядов после вылета из канала ствола вызывается различием атмосферных условий; формы, весов, положений центра тяжести снарядов; окраски и смазки наружной поверхности снарядов; влияния последействия газов и др. Увеличение рассеивания снарядов снижает точность стрельбы и ведет к увеличению их расхода и времени на выполнение огневой задачи.

Рассеивание снарядов — явление неизбежное. Однако исследование причин рассеивания снарядов показывает, что значительная часть из них зависит от правильного хранения, сбережения и подготовки орудий и боеприпасов к стрельбе и от обученности личного состава орудийных расчетов выполнению своих обязанностей.

Кучностьесть свойство, обратное рассеиванию. Чем меньше рассеивание, тем больше кучность т. е. тем больше сосредоточены (скучены) траектории (точки падения) между собой. Если мерой рассеивания служат срединные отклонения Вд, Вб, Вв, то мерой кучности, как явления, обратного рассеиванию, должны служить величины, обратные срединным отклонениям, т. е. ; ; .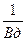

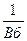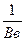Во сколько раз срединные отклонения больше, во столько же раз больше и рассеивание и во столько же раз меньше кучность, и наоборот.

Подметкостьюстрельбы понимают отклонение центра группирования от центра цели.

Меткость зависит от ошибок наводки, ошибок таблиц стрельбы, определения условий стрельбы и ошибок пристрелки. При отсутствии указанных ошибок, чем лучше кучность, тем выше меткость орудия, поскольку вероятность попадания при одном выстреле в цель заданных размеров возрастает. Это положение имеет особое значение при стрельбе прямой наводкой по целям малых размеров (например, по танкам). Вследствие этого к орудиям, предназначенным для стрельбы прямой наводкой по таким целям, предъявляется требование высокой кучности. При высокой кучности с целью повышения меткости стрельбы танковой и противотанковой артиллерии, а также орудий полевой артиллерии, имеющих прицел прямой наводки, производится приведение каждого орудия к нормальному бою путем их пристрелки.