Зображення графів

Визначення. Граф G називається неорієнтованим, якщо кожне його ребро є неорієнтованим. Граф G називається орієнтованим, якщо кожне його ребро є орієнтованим.

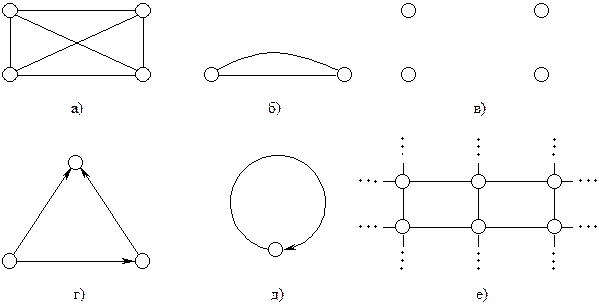
Рис. 1.

На рис. 1.а, б, в, е зображені деякі неорієнтовані графи, а на рис. 1.г, д – деякі орієнтовані графи (напрями ребер зображені стрілками). Лінії, які відповідають ребрам графів, можуть перетинатись на рисунку, але точки їх перетину не обов’язково повинні бути вершинами графу (див.рис.1.а).

Якщо два ребра інцидентні одній парі вершин, то такі ребра називаються кратними (див.рис.1.б). Ребро, яке з’єднує вершину саму з собою, називають петлею (див.рис.1.д).

Визначення. Граф називається скінченним, якщо кількість ребер в ньому є скінченною (рис.1.а, б, г); інакше граф називають нескінченним (рис.1.е).

Визначення. Вершина графу, не інцидентна жодному ребру, називається ізольованою. Якщо граф складається тільки з ізольованих вершин, то він називається нульграфом (рис.1.в).

Визначення. Будемо говорити, що два графи G і G’ є ізоморфними, якщо існує така відповідність між множинами їх вершин V і V’, що у графі G вершини з’єднані між собою тоді і тільки тоді, коли з’єднані між собою відповідні їм вершини у графі G’. Якщо ребра орієнтовані, то їх напрямки повинні відповідати один одному.

Наприклад:

Твердження. Ізоморфні графи мають однакові властивості.

Відповідно з даними твердженнями ізоморфні графи надалі будемо ототожнювати.