Симметрия кристаллов

Цель модуля: Познакомить студентов с принципами классификации кристаллов по их симметрии, показать связь между симметрией кристаллов, их морфологией и физическими свойствами, дать понятие о истинной и видимой симметрии, как результате сложения симметрии кристаллической решетки и симметрии кристаллообразующей среды, познакомить с механизмами образования различных форм кристаллических агрегатов.

В предыдущей лекции говорилось об особых свойствах кристаллов, отличающих их от аморфных тел. Исходя из всего вышеизложенного, можно дать следующее определение: «Кристаллами называют твердые тела, обладающие трехмерно-периодической упорядоченной пространственной структурой и имеющие вследствие этого форму правильных многогранников».

Существует бесчисленное множество таких многогранников как среди природных минералов, так и выращенных в лабораториях, поэтому для их систематического изучения необходимо выделить определенные критерии, присущие всем без исключения кристаллам, но позволяющие их объединить в группы, укладывающиеся в четкую классификацию. Одним из таких критериев является симметрия, как особый вид пространственной идентичности объемных фигур. В кристаллографии термин «симметрия» подразумевает соразмерность, закономерное повторение в пространстве одинаковых элементов ограничения кристалла, его граней, ребер и вершин.

Симметрию кристаллов можно описать, используя вспомогательные символы – элементы симметрии. К ним относятся – центр симметрии, плоскости симметрии и оси симметрии. Путем несложных манипуляций можно найти элементы симметрии, составить кристаллографическую формулу кристалла и определить вид его симметрии.

Во всех учебниках и учебно-методических руководствах по геометрической кристаллографии вопросам симметрии кристаллов уделяется много внимания. Техника определения элементов симметрии отрабатывается в процессе лабораторных занятий с использованием моделей-имитаторов кристаллов. Поэтому мы ограничимся лишь общими формулировками и выводами, дающими возможность классифицировать кристаллы и даже прогнозировать проявления некоторых их свойств.

Следует всегда иметь в виду, что симметрия кристалла является функцией его кристаллической структуры. Поэтому, определяя принадлежность кристалла к определенному виду симметрии, мы тем самым идентифицируем его кристаллическую структуру, относя ее к определенной категории, что позволяет построить достаточно четкую и удобную для практического применения классификацию.

Итак, симметрию кристалла можно описать, используя вспомогательные символы – элементы симметрии. Стоит ли говорить, что эти вспомогательные символы (образы) в реальном физическом воплощении не существуют, поэтому в формулировках их определений всегда можно добавить слово «воображаемый» (воображаемая точка, воображаемая плоскость, воображаемая ось).

Дадим определения основным элементам симметрии:

Центр симметрии (центр обратного равенства, центр инверсии). Центром симметрии называют воображаемую точку, находящуюся внутри кристалла, в которой пересекаются и делятся пополам линии, соединяющие одинаковые элементы ограничения кристалла (середины граней, ребер, противоположные вершины).

Другое, аналогичное по смыслу определение. Центром симметрии называют воображаемую точку внутри кристалла, по обе стороны от которой на равном расстоянии находятся одинаковые элементы ограничения кристалла.

Обозначается центр симметрии латинской буквой «С».

Все существующие кристаллы можно разделить на две группы – те, в которых центр есть, и те, в которых центра симметрии нет. Если в кристалле центр симметрии есть, то он всегда только один и обязательно находится внутри кристалла.

Плоскости симметрии. Плоскостью симметрии называют такую воображаемую плоскость, которая делит кристалл на две зеркально-равные части. Последнее обстоятельство следует подчеркнуть особо, поскольку половинки кристалла после пересечения их плоскостью должны выглядеть как предмет и его зеркальное отражение.

Плоскости симметрии обозначаются латинской буквой «Р». В одном кристалле может быть различное число плоскостей симметрии. Их может вообще не быть, но может насчитываться до девяти. Большего количества плоскостей симметрии в кристаллах не бывает.

Оси симметрии. Осью симметрии называется такая воображаемая ось, при повороте вокруг которой на определенный угол, кристалл совмещается в пространстве сам с собой. Наименьший угол, при котором происходит такое совмещение, называется элементарным углом поворота (α).

Число совмещений в пространстве, которое можно получить при повороте кристалла вокруг оси на 360^о определяет порядок оси симметрии. Оси обозначаются буквой «L».

Если при полном обороте кристалла вокруг оси произойдет только одно совмещение (т.е. α = 360^о ), то мы имеем ось первого порядка (L₁). Таких осей в любом, даже самом несимметричном кристалле может быть бесчисленное множество, и при описании симметрии кристалла они не учитываются.

Если при полном обороте кристалла произойдет два совмещения (α = 180^о), то мы имеем ось второго порядка (L₂).При трех совмещениях (α =120^о) мы получим ось третьего порядка (L₃). При четырех совмещениях (α =90^о) – получим ось четвертого порядка (L₄). И, наконец, при шести совмещениях (α = 60^о) получится ось шестого порядка (L₆). Математически доказано, что осей пятого порядка (L₅) быть не может.

В одном кристалле возможно сочетание нескольких осей симметрии различных порядков.

Совокупность всех имеющихся в кристалле элементов симметрии составляет его кристаллографическую формулу или вид симметрии (например, для куба -3L₄4L₃6L₂9PC ).

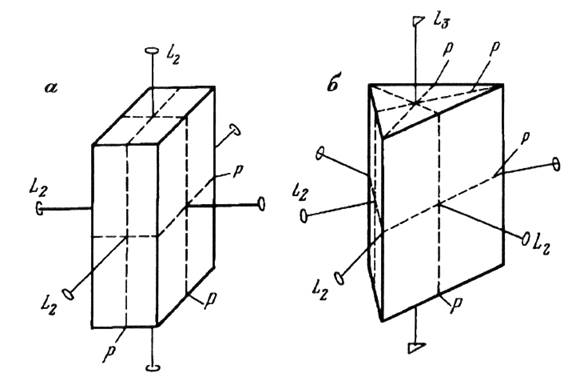
Рис. 1 Многогранники с разными наборами элементов симметрии