Поляризация электромагнитной волны
Рассмотрим плоскую гармоническую волну. Каждая из компонент меняется по закону косинуса, т.е.
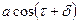 (6.35)
(6.35)
где 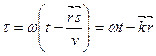 (6.36)
(6.36)
Пусть волна распространяется вдоль оси 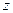 . Тогда, вследствие поперечности электромагнитной волны, у неё будут только компоненты
. Тогда, вследствие поперечности электромагнитной волны, у неё будут только компоненты 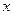 и
и 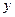 (вектор
(вектор 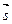 направлен вдоль оси
направлен вдоль оси 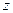 ).
).
Рассмотрим кривую, которую описывает конец вектора 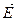 в произвольной точке пространства. Эта кривая является геометрическим местом точек, координаты которых равны:
в произвольной точке пространства. Эта кривая является геометрическим местом точек, координаты которых равны:
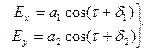 (6.37)
(6.37)
Преобразуем уравнения:
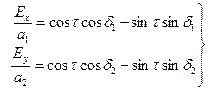 (6.38)
(6.38)
Следовательно,
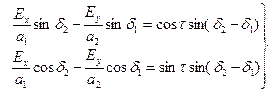 (6.39)
(6.39)
Возведя в квадрат каждое из уравнений (5.44), и сложив их, получим следующее выражение:
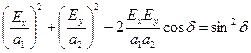 , (6.40)
, (6.40)
где 
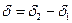
Уравнение (6.40) носит название канонического сечения. Геометрическое место точек концов вектора напряженности электрического поля в общем случае представляет эллипс, который вписан в прямоугольник со сторонами 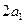 и
и 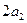 . В этом случае говорят, что волна эллиптически поляризована (рис. 6.3(a)).
. В этом случае говорят, что волна эллиптически поляризована (рис. 6.3(a)).
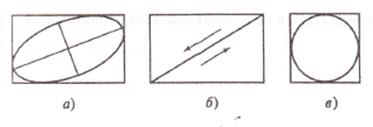
Рис. 6.3. Световая волна эллиптической поляризации при разных значениях 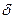 : (а) –
: (а) – 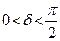 ; (б) –
; (б) – 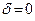 ; (в) –
; (в) – 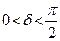 ,
,  .
.
В частном случае эллипс канонического сечения может выродиться либо в прямую линию (рис. 6.3(б)), либо в окружность (рис. 6.3(в)). В этих случаях имеет место линейная или круговая поляризация. Круговая поляризация, в зависимости от направления движения по окружности, может быть правой или левой.
Распространение света в усиливающей среде. Уравнения Максвелла-Блоха
Активное волокно эрбиевых усилителей может быть упрощенно описано моделью двухуровневых частиц. Взаимодействие двухуровневой системы со световой волной описывается хорошо известными уравнениями Максвелла-Блоха []. Применим их к описанию волоконного усилителя. Следуя работе [ссылка 68 у Агравала] включим в выражение для поляризации 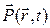 член
член 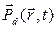 , описывающий вклад легирующих примесей (dopants). Этот вклад рассчитывается на основе полуклассического подхода к описанию взаимодействия оптического поля
, описывающий вклад легирующих примесей (dopants). Этот вклад рассчитывается на основе полуклассического подхода к описанию взаимодействия оптического поля 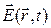 , который наводит в частицах примесей дипольный момент. В приближении медленно меняющейся огибающей выражение для
, который наводит в частицах примесей дипольный момент. В приближении медленно меняющейся огибающей выражение для 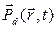 имеет следующий вид.
имеет следующий вид.
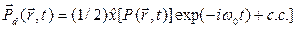 ,
,
где 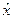 - единичный вектор, связанный с поляризацией поля
- единичный вектор, связанный с поляризацией поля 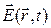 . Медленно меняющаяся часть
. Медленно меняющаяся часть 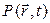 определяется решением уравнений Блоха, которые могут быть записаны в следующем виде.
определяется решением уравнений Блоха, которые могут быть записаны в следующем виде.
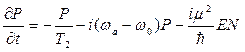 , (МБ1)
, (МБ1)
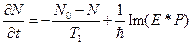 , (МБ2)
, (МБ2)
где 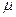 - дипольный момент,
- дипольный момент, 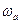 - частота излучения атомного перехода,
- частота излучения атомного перехода, 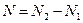 - плотность инверсной населенности с начальным значением
- плотность инверсной населенности с начальным значением 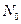 ,
, 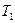 и
и 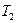 - времена релаксации инверсной населенности и поляризации,
- времена релаксации инверсной населенности и поляризации, 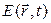 - медленно меняющаяся амплитуда, связанная с электрическим полем. Опустив выкладки приведем окончательное выражение для уравнения, описывающего эволюцию оптического импульса в усиливающей двухуровневой среде:
- медленно меняющаяся амплитуда, связанная с электрическим полем. Опустив выкладки приведем окончательное выражение для уравнения, описывающего эволюцию оптического импульса в усиливающей двухуровневой среде:
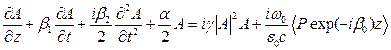 (МБ3)
(МБ3)
где угловые скобки означают пространственное усреднение по сечению моды 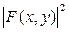 . Если линия уширена неоднородно, то необходимо провести усреднение по частотам атомного перехода
. Если линия уширена неоднородно, то необходимо провести усреднение по частотам атомного перехода
Систему уравнений Максвелла – Блоха (МБ1-3) необходимо использовать при анализе распространения импульсов с длительностью меньшей или сопоставимой с временем релаксации диполей ( 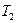 <0,1 пс). При описании импульсов большей длительности анализ существенно упрощается, т.к. можно использовать приближение скоростных уравнений, в котором предполагается что время отклика примесей настолько быстрое, что индуцированная поляризация адиабатически наводится электрическим полем [8 из Агравала].
<0,1 пс). При описании импульсов большей длительности анализ существенно упрощается, т.к. можно использовать приближение скоростных уравнений, в котором предполагается что время отклика примесей настолько быстрое, что индуцированная поляризация адиабатически наводится электрическим полем [8 из Агравала].
Чтобы учесть дисперсионные эффекты, связанные с наличием активных примесей, необходимо перейти в спектральное представление и определить поляризуемость частиц примеси стандартным выражением
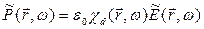 ,
,
где 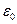 - пояризуемость вакуума, а тильда означает преобразование Фурье. В этом представлении поляризуемость имеет вид
- пояризуемость вакуума, а тильда означает преобразование Фурье. В этом представлении поляризуемость имеет вид
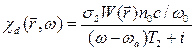 ,
,
где сечение перехода 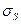 связано с дипольным моментом
связано с дипольным моментом 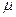 следующим соотношением:
следующим соотношением: 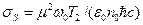 , и
, и 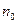 - линейный показатель преломления матрицы на частоте
- линейный показатель преломления матрицы на частоте 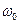 .
.
Уравнение Ландау-Гинзбурга
Распространение световых сигналов в оптическом усилителе описывается системой уравнений Б1-Б5. Главная особенность распространения света в двухуровневой среде состоит в том, что 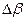 оказывается частотно зависимым из-за частотной зависимости поляризуемости
оказывается частотно зависимым из-за частотной зависимости поляризуемости 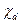 . Для перехода из частотной области во временную необходимо разложить
. Для перехода из частотной области во временную необходимо разложить 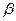 и
и 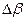 в ряд Тейлора включив в рассмотрение эффекты, связанные с примесями. Воспользовавшись представлением
в ряд Тейлора включив в рассмотрение эффекты, связанные с примесями. Воспользовавшись представлением 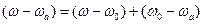 и воспользовавшись обобщенным разложением в ряд Тэйлора можно получить следующее уравнение [69 из Агравала]:
и воспользовавшись обобщенным разложением в ряд Тэйлора можно получить следующее уравнение [69 из Агравала]:
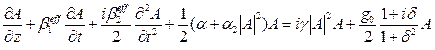 (…)
(…)
где
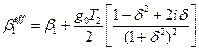 ,
,
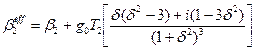 ,
,
а параметр расстройки 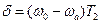 . Усиление
. Усиление 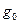 определяется выражением:
определяется выражением:
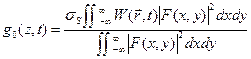


Спектры поглощения и люминесценции
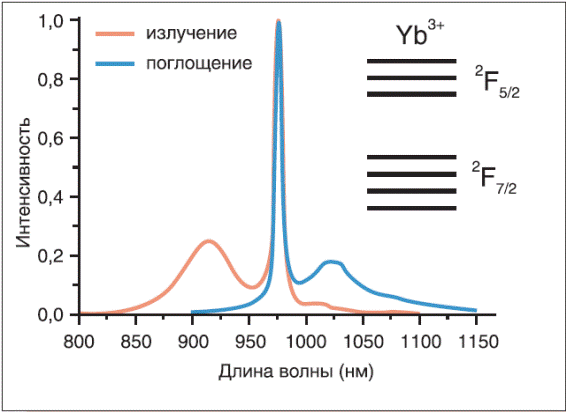
Рис. 2. Спектры излучения и поглощения
ионов Yb3+ в алюмосиликатном световоде.
Справа вверху – схема уровней
Дата добавления: 2015-06-12; просмотров: 1068;
