Диагностические модели
Обеспечить требуемый уровень приспособленности объекта к диагностированию можно только в том случае, если уже с первого этапа его проектирования будут учитываться требования технической диагностики.
В общем случае под ОД понимается динамическая система (рис.15.1), y(t) преобразующая совокупность входных воздействий 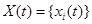
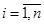 совокупность выходных реакций
совокупность выходных реакций 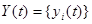 ,
, 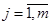
 Входные воздействия включают рабочие и тестовые сигналы, и помехи. Совокупность внутренних переменных
Входные воздействия включают рабочие и тестовые сигналы, и помехи. Совокупность внутренних переменных 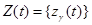 ,
, 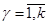 представляет собственные параметры объекта, определяющие его свойства как преобразователя Х(t) в Y(t), т.е. Y(t) = Z(t)Х(t).
представляет собственные параметры объекта, определяющие его свойства как преобразователя Х(t) в Y(t), т.е. Y(t) = Z(t)Х(t).
Если зафиксировать входные воздействия в установленных пределах, то выходная реакция ОД должна быть в пределах области работоспособности в случае его работоспособного состояния. Если же при нормальном входном сигнале Y(t) выходит за установленные пределы, то произошли изменения свойств объекта, связанные с изменением Z(t).
Поскольку требуется выбрать диагностические признаки ОД, когда он еще физически отсутствует, то для этой цели приходится использовать его модель или модели. Под модельюобычно понимается упрощенный абстрактный или физический образ реального объекта (оригинала), подлежащего изучению. Следовательно, модель – приближенная копия оригинала, отображающая его определенные свойства, наиболее важные с точки зрения решаемой проблемы. На практике разрабатываются такие модели, которые представляют собой гомоморфный (частично соответствующий) образ объекта исследования и изоморфный (полностью соответствующий) образ его изучаемых свойств и характеристик.
Анализ объекта с целью определения его состояния предполагает построение математической модели. Теоретический анализ ОД при решении задач диагностирования предполагает некоторую идеализацию, которая абстрагирует подходящим образом выбранные существенные свойства объекта. Реальный объект при этом заменяется диагностической моделью (ДМ).
Оценка состояния ЭУ осуществляется по диагностическим признакам (параметрам и характеристикам). Обычно в качестве диагностических параметров принимаются параметры ДМ. В этом случае выбор или построение адекватной ДМ имеет существенное значение для оценивания состояния ЭУ.
В соответствии с ГОСТ 20911-89 диагностическая модель – формализованное описание объекта диагностирования, необходимое для решения задач диагностирования. Описание может быть представлено в аналитической, табличной, векторной, графической или другой форме.
ДМ в общем случае определяет зависимость выходных параметров (сигналов) объекта от его структурных (диагностических) параметров и входных сигналов. В некоторых случаях ДМ учитывают время.
ДМ могут иметь различный вид. Для описания ЭУ в основном применяются алгебраические уравнения (линейные и нелинейные), дифференциальные уравнения, передаточные функции, характеристические уравнения, графы и диаграммы прохождения сигналов, булевы функции.
Аппарат булевой алгебры, в основном, применяется для определения работоспособности и поиска дефектов в дискретных объектах. Такими объектами являются системы управления ЭУ, регулирования и защиты трансформаторов, электрических машин, воздушных линий, а также система контроля и проверки цепей релейной защиты автоматики.
В связи с большим разнообразием элементов ЭУ, как по назначению и режимам использования, так и по принципам построения и конструкции, разработчикам СД приходится использовать большое число различных ДМ. Чтобы облегчить выбор вида ДМ для конкретного оборудования на стадии его разработки, целесообразно классифицировать эти модели. Из всех возможных принципов построения системы классификации приведем классификацию диагностических моделей, основанную на методах их анализа. Такая классификация позволяет ориентировать разработчика при выборе ДМ на определенные методы их анализа и соответственно на использование конкретного математического аппарата.
По методам представления связей между состояниями объекта, его элементами и параметрами все ДМ, которые могут найти применение для описания электрооборудования, разбиваются на три группы: непрерывные, дискретные и специальные. Рассмотрим каждую из групп моделей отдельно.
Непрерывные диагностические модели. Непрерывными моделями оборудование проеставляют в том случае, когда рассматриваемые процессы протекают непрерывно или в непрерывно изменяющемся времени, которое является аргументом соответствующих функций. Такие модели объединяют линейные и нелинейные алгебраические и дифференциальные уравнения, передаточные функции и характеристические уравнения.
Алгебраически уравнения. Наиболее простыми ДМ являются линейные алгебраические уравнения, описывающие установившиеся (статические) процессы. Коэффициенты этих уравнений являются параметрами, характеризующими состояние объекта. В данном случае задача диагностирования сводится к оцениванию коэффициентов непосредственно или косвенно и сравнению с допустимыми значениями.
В общем случае такая модель записывается в виде:
Y = AX, (15.1)
где X – совокупность входных воздействий; Y – совокупность реакций ОД; A – оператор преобразования Х в Y;
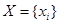 ,
, 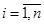 ;
; 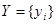 ;
; 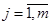
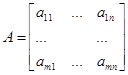 .
.
Если aij = const, то объект описывается линейными алгебраическими уравнениями, если aij = f(x), то объект описывается нелинейными уравнениями.
Собственно состояние объекта оценивает оператор А, структура и параметры которого определяют показатели качества работы объекта. При этом задачи контроля работоспособности и поиска дефектов решаются контролем соответствия действительного оператора А требуемому Ао.
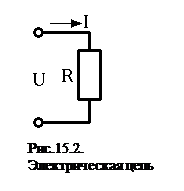
В простейшем случае (рис.15.2) уравнение (15.1) имеет вид:
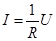 ,
,
где 1/R = а – коэффициент уравнения.
Задача анализа таких моделей сводится к определению коэффициентов аij, которые являются прямыми диагностическими параметрами.
 Дифференциальные уравнения. Наиболее широкое применение для описания процессов функционирования элект-рооборудования получили дифференциальные уравнения. Коэффициенты дифференциальных уравнений являются диагностическими параметрами. Они позволяют выявить дефекты, появляющиеся в динамических режимах. Задача диагностирования состоит в определении коэффициентов дифференциального уравнения (передаточных коэффициентов и постоянных времени) и сравнении их с допустимыми значениями.
Дифференциальные уравнения. Наиболее широкое применение для описания процессов функционирования элект-рооборудования получили дифференциальные уравнения. Коэффициенты дифференциальных уравнений являются диагностическими параметрами. Они позволяют выявить дефекты, появляющиеся в динамических режимах. Задача диагностирования состоит в определении коэффициентов дифференциального уравнения (передаточных коэффициентов и постоянных времени) и сравнении их с допустимыми значениями.
В общем виде такие ДМ для динамического объекта с одним входным воздействием х(t) и одним выходным сигналом y(t) имеют вид:
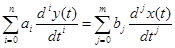
с некоторыми начальными условиями
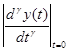 ,
, 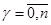 ,
,
где аi, bj – коэффициенты (прямые диагностические параметры) уравнений, m < n.
Такое представление достаточно универсально, т.к. если коэффициенты аi и bj постоянны, то уравнение определяет поведение линейного динамического объекта с сосредоточенными параметрами.
В случае зависимости коэффициентов от времени аi = аi(t) и bj = bj(t) уравнение определяет поведение любого объекта с переменными параметрами, который можно отнести к классу линейных нестационарных объектов. Если аi = аi(y) и bj = bj(x), то уравнение является описанием нелинейного нестационарного объекта. И, наконец, если аi = аi(y,t) и bj = bj(x,t), то уравнение служит описанием нелинейного нестационарного объекта.
К сожалению, в двух последних случаях отсутствуют аналитические методы решения дифференциального уравнения в общем виде даже для известных функций аi(y) и bj(x).
Априорные сведения о процессах, происходящих в объекте, позволяют упростить (линеаризировать) нелинейные уравнения, что позволит использовать доступные методы анализа линейных дифференциальных уравнений. Простым примером такой модели являются уравнения, описывающие работу схемы (рис.15.3) при подаче на вход сигнала включения u = Uо1(t)
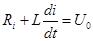
Схемы замещения 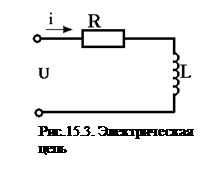 находят применение в качестве ДМ электрооборудования. При этом структурные параметры схемы замещения являются диагностическими. Они несут определенный физический смысл и наиболее полно отражают состояние электрооборудования.
находят применение в качестве ДМ электрооборудования. При этом структурные параметры схемы замещения являются диагностическими. Они несут определенный физический смысл и наиболее полно отражают состояние электрооборудования.
Среди электрооборудования наиболее многочисленной группой являются электрические машины. Их можно разделить на три группы: машины переменного тока, машины постоянного тока и трансформаторы. Модели электрических машин обычно представляют схемами замещения.
Наиболее распространенная модельтрансформатора в виде схемы замещения приведена на рис.15.4. Рассмотренная схема может быть заменена так называемой "приведенной схемой" (рис.15.5).
Дифференциальные уравнения, описывающие переходный процесс в трансформаторе, примут вид:
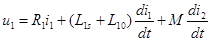 .
.
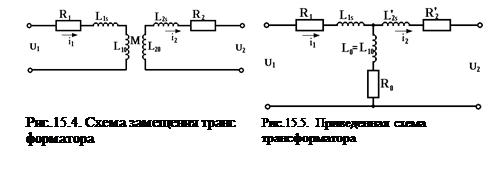
Диагностические параметры в этом случае – R1, R2, L1s, L2s, L10, L20. Параметр М не является прямым диагностическим параметром, так как определяется через другие зависимостью
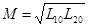 .
.
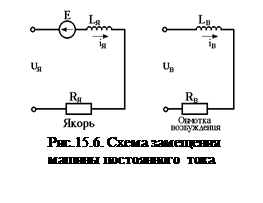 Схема замещения машины постоянного тока имеет вид, представленный на рис.15.6.
Схема замещения машины постоянного тока имеет вид, представленный на рис.15.6.
Переходный процесс в этом случае описывается дифференциальными уравнениями вида
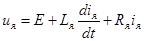 ;
; 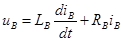 .
.
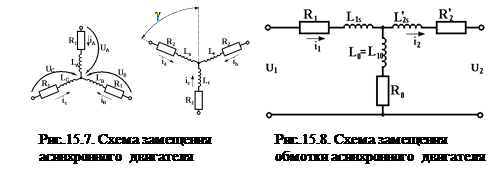
Диагностическими параметрами для машины постоянного тока являются Lя, Rя, Lв, Rв.Модель асинхронного двигателя можно представить схемой замещения (рис.15.7).
Учитывая симметрию фаз, в качестве модели можно использовать приведенную схему замещения одной фазы асинхронного двигателя (рис.15.8).
Диагностическая модель асинхронного двигателя представлятся в виде
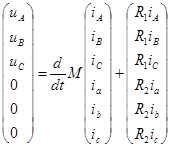
Прямыми диагностическими параметрами в этом случае являются L1s, L2s, L10, L20, R1, R2, косвенным диагностическим параметром – взаимоиндуктивность 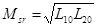 . Матрица взаимоиндуктивностей приведена в табл. 15.1.
. Матрица взаимоиндуктивностей приведена в табл. 15.1.
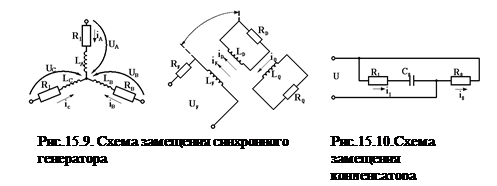
Наиболее сложная модель функционирования у синхронного генератора, схема замещения которого представлена на рис.15.9. 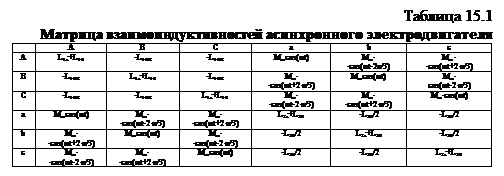
Матрица взаимоиндуктивностей приведена в табл.15.2. Уравнения, описывающие электромагнитные процессы в синхронном генераторе, имеют вид
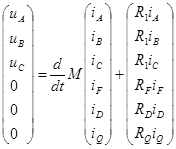
В ЭУ широкое распространение для фильтрации высших гармоник, компенсации реактивной мощности получили конденсаторы, схема замещения которых имеет вид (рис.15.10).
Дифференциальные уравнения, описывающие переходной процесс в конденсаторе при подаче сигнала, имеют вид:
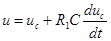 ;
; 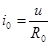 ;
; 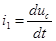 .
.
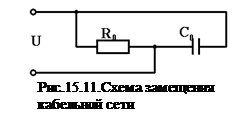
Надежность ЭУ существенно зависит от состояния кабельных сетей. Как правило, в качестве моделей сетей используются сети с распределенными параметрами. Для диагностирования кабельной линии со сравнительно малой протяженностью при оценивании изоляции можно использовать схему замещения, представленную на рис.15.11.
При необходимости учета дополнительных физических явлений в электрооборудовании рассмотренные модели могут усложняться. Чем больше факторов учитывает модель и более адекватно описывается объект, тем сложнее ДМ. Однако часто анализ ДМ сложного объекта затруднен, поэтому необходимо разбить ОД на структурные единицы, математическое описание которых не представляет трудности.
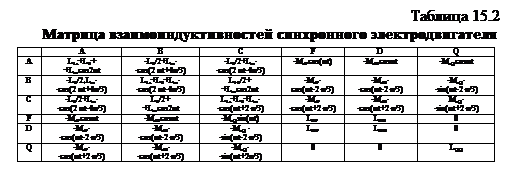
Передаточная функция. Разновидностью ДМ на основе дифференциального уравнения является передаточная функция:
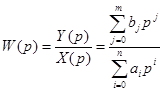 ,
,
определяемая отношением Y(p) и X(p) преобразованием Лапласа выходного Y(t) и входного X(t) процессов.
Передаточная функция оценивает как качественную, так и количественную стороны изменения состояния ОД. Характер структурного построения передаточной функции выражает качественную сторону (колебательный, апериодический характер процесса), а основные параметры – количественные изменения, происходящие в ОД. Следовательно, контролируя степень изменения основных параметров W(p), можно судить об изменении работоспособности ОД. На практике для диагностирования такая модель используется до 3-го порядка.
 Характеристические уравнения. Следует иметь в виду, что в дифференциальном уравнении коэффициенты bj определяют лишь относительную величину составляющей выходного сигнала, в то время как коэффициенты аi – собственные частоты объекта и характер изменения выходного сигнала объекта. Поэтому, в первую очередь, следует обращать внимание на вычисление коэффициентов левой части дифференциального уравнения, которая представляет разновидность ДМ – характеристическое уравнение
Характеристические уравнения. Следует иметь в виду, что в дифференциальном уравнении коэффициенты bj определяют лишь относительную величину составляющей выходного сигнала, в то время как коэффициенты аi – собственные частоты объекта и характер изменения выходного сигнала объекта. Поэтому, в первую очередь, следует обращать внимание на вычисление коэффициентов левой части дифференциального уравнения, которая представляет разновидность ДМ – характеристическое уравнение
аnрn + аn-1рn-1 +...+ а1р + ао = 0.
Решение такого уравнения позволяет определить коэффициенты (прямые диагностические признаки) через его корни. В зависимости от расположения полюсов – корней уравнения – определяется состояние ОД.
Линейная система устойчива по теореме Ляпунова, если полюса лежат в левой полуплоскости р1, р2 (рис.15.12), т.е. мнимая ось является границей устойчивости.
Если полюса расположены на мнимой оси (р3,р4), то в объекте существуют колебания (амплитуда колебаний постоянна, если полюса 1-го порядка). Полюса в правой полуплоскости (р5,р6) свидетельствуют об экспоненциальном нарастании колебаний и объект оказывается неустойчивым.
Следовательно, по расположению полюсов можно судить о работоспособности ОД.
 Дискретные диагностические модели. Эти модели определяют состояние оборудования только для последовательности дискретных значений независимой переменной (времени), но без учета характера процесса в промежутках. Их можно представить конечно-разностными уравнениями или конечными автоматами.
Дискретные диагностические модели. Эти модели определяют состояние оборудования только для последовательности дискретных значений независимой переменной (времени), но без учета характера процесса в промежутках. Их можно представить конечно-разностными уравнениями или конечными автоматами.
Конечно-разностные уравнения. Такие уравнения связывают значения yk (рис.15.13) функции y = f(x) на дискретном множестве значений xk и записываются в общем виде:
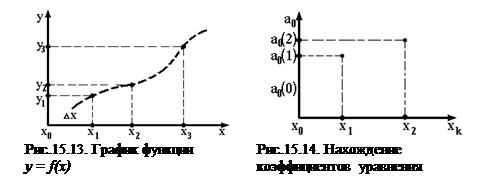 |
yk = f(yk-1,...,y1,xk), k = 0,1,2,3,...
Причем интервал 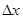 между дискретными значениями xk может быть постоянным или изменяться.
между дискретными значениями xk может быть постоянным или изменяться.
Обыкновенное разностное уравнение, используемое в качестве ДМ, имеет вид:
ао(k)yk+r + а1(k)yk+r-1 +...+ аr(k)yk = хk, r = 1,2,3,...
Если аr = const,то уравнение линейное, если аr = f(xk),то – нелинейное. Как и в ранее рассмотренных ДМ коэффициенты аr характеризуют изменение состояния ОД. Решить уравнение значит найти его коэффициенты.
Например, для r = 2 уравнение имеет вид:
ао(k)yk+2 + а1(k)yk+1 + а2(k)yk = хk,
Известны значения входной и выходной переменных в точках 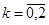 .
.
Дата добавления: 2015-06-10; просмотров: 2742;
