Опис стану за допомогою хвильової функції. Рівняння Шредінгера.
Так як з мікрочастинкою співставляють хвильовий процес, який відповідає її рухові, то стан частинки в квантовій механіці описується хвильовою функцією, залежною від координати і часу:  .
.
Інтенсивність хвиль де Бройля визначається величиною квадрата модуля хвильової функції 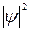 .
.
З дослідів по дифракції електронів випливає, що інтенсивність хвиль у певній точці простору визначає число електронів, що потрапили в цю точку за 1 с. Це стало основою для своєрідного імовірнісного тлумачення хвиль де Бройля. Ймовірність того, що частинка знаходиться в елементі об’єму  , пропорційна
, пропорційна 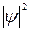 і елементу об’єму
і елементу об’єму
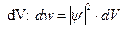
|
Величина 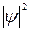 є густиною ймовірності
є густиною ймовірності
і задає ймовірність перебування частинки в даній точці простору.
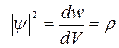
| (7.7) |
В квантовій механіці існують обмеження в можливостях одночасного визначення координати частинки і величини її імпульсу. Ці обмеження пов’язані з хвильово – корпускулярним дуалізмом мікрочастинок. Гейзенберг показав, що чим точніше визначена одна з двох змінних величин, які визначають стан мікрочастинки, тим з меншою точністю може бути визначена друга з них і навпаки. Добуток похибок, з якими визначаються ці величини, не може бути менше сталої Планка 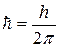 . Наприклад, якщо координата х частинки визначена з похибкою
. Наприклад, якщо координата х частинки визначена з похибкою 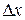 , то імпульс частинки
, то імпульс частинки 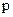 визначається з похибкою
визначається з похибкою 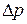 , більший, або рівний сталій Планка:
, більший, або рівний сталій Планка:

| (7.8) |
Аналогічне співвідношення є для при визначенні енергії 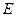 і часу
і часу 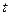 , на протязі якого частинка має цю енергію:
, на протязі якого частинка має цю енергію:
 . .
| (7.9) |
В квантовій механіці дію на об’єкти в процесі вимірювання не можна вважати малою або несуттєвою – стан об’єкту при вимірюванні змінюється. Наприклад, для визначення положення електрона його необхідно “освітити” світлом можливо більш високої частоти. В результаті співудару електрона з фотоном імпульс електрона зміниться на величину:  .
.
Рівняння Шредінгера та його розв’язок для атома водню. Квантові числа.
Після відкриття в 1927р. Гейзенбергом співвідношення невизначеностей постало питання створення квантової теорії руху частинок, оскільки виявилися принципова неможливість описати рух частинок за допомогою поняття траєкторії. Стан мікрочастинок описується  - функцією, яка визначається рівнянням Шредінгера, яке відіграє в квантовій механіці таку ж роль, як і рівняння Ньютона в класичній механіці. Образно кажучи, Шредінгер перевів уявлення класичної механіки на мову квантової теорії. За допомогою хвильового рівняння Шредінгера можна описати еволюцію
- функцією, яка визначається рівнянням Шредінгера, яке відіграє в квантовій механіці таку ж роль, як і рівняння Ньютона в класичній механіці. Образно кажучи, Шредінгер перевів уявлення класичної механіки на мову квантової теорії. За допомогою хвильового рівняння Шредінгера можна описати еволюцію 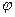 - функції, якщо вона відома в якийсь момент часу.
- функції, якщо вона відома в якийсь момент часу.
Якщо  - функція не залежить від часу
- функція не залежить від часу 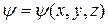 вона задовольняє стаціонарному рівнянню Шредінгера, яке для одномірного випадку має вигляд:
вона задовольняє стаціонарному рівнянню Шредінгера, яке для одномірного випадку має вигляд:
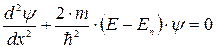
| (7.10) |
де 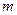 – маса частинки,
– маса частинки, 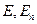 - її повна і потенціальна енергія.
- її повна і потенціальна енергія.
Функції  , які задовільняють рівняння Шредінгера при заданому вигляді
, які задовільняють рівняння Шредінгера при заданому вигляді  , називаються власними функціями. Вони існують лише при певних значеннях енергії. Сукупність власних значень енергії утворює енергетичний спектр частинки. Знаходження власних значень і власних функцій складає основну задачу квантової механіки.
, називаються власними функціями. Вони існують лише при певних значеннях енергії. Сукупність власних значень енергії утворює енергетичний спектр частинки. Знаходження власних значень і власних функцій складає основну задачу квантової механіки.
Опис стану атомів і молекул з допомогою рівняння Шредінгера є досить складною задачею. Найпростіше вона розв’язується для одного електрона в полі ядра. Проте і в цьому випадку розв’язок виходить за межі нашого курсу, тому ми обмежимося якісним розглядом питання.
При центральній симетрії поля, створеного ядром, задачу зручно розв’язувати у сферичних координатах 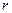 ,
,  і
і 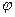 . Розв’язок рівняння Шредінгера знаходять у вигляді добутку трьох функцій, кожна з яких залежить від однієї змінної
. Розв’язок рівняння Шредінгера знаходять у вигляді добутку трьох функцій, кожна з яких залежить від однієї змінної
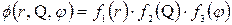
| (7.11) |
Загальний розвиток є дискретним, тобто кожна з функцій 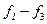 має набір (спектр) розв’язків, кожному з яких відповідає певне квантове число.
має набір (спектр) розв’язків, кожному з яких відповідає певне квантове число.
Перше з них – головне квантове число 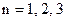 ... .Воно визначає рівні енергії електрона по закону
... .Воно визначає рівні енергії електрона по закону
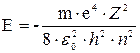
| (7.12) |
Цей вираз є розв’язком рівняння Шредінгера і повністю співпадає з відповідною формулою теорії Бора.
Друге квантове число – орбітальне  , яке при даному n може приймати значення
, яке при даному n може приймати значення 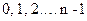 . Це число характеризує орбітальний момент імпульса
. Це число характеризує орбітальний момент імпульса 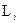 електрона відносно ядра:
електрона відносно ядра:
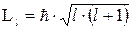
| (7.13) |
Третє квантове число – магнітне m, яке при даному l приймає значення 0, 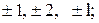 всього
всього 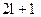 значень.
значень.
Це число визначає проекції орбітального момента імпульса електрона на довільно вибраний напрям Z :
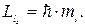
| (7.14) |
Четверте квантове число – спінове 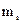 . Воно може приймати тільки два значення
. Воно може приймати тільки два значення 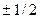 і характеризує можливі значення проекції спіна електрона :
і характеризує можливі значення проекції спіна електрона :
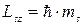
| (7.15) |
Стан електрона в атомі з відомими n і  позначають таким чином 1S, 2S, 3P, 3S і т. д. Тут цифра вказує значення головного квантового числа, а буква – орбітальне квантове число: символам
позначають таким чином 1S, 2S, 3P, 3S і т. д. Тут цифра вказує значення головного квантового числа, а буква – орбітальне квантове число: символам  … відповідають значення l=0, 1. 2, 3..і т. д.
… відповідають значення l=0, 1. 2, 3..і т. д.
Число станів з даними n і  буде
буде 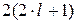 . Щоб знайти загальне число станів з однаковим головним квантовим числом n, просумуємо
. Щоб знайти загальне число станів з однаковим головним квантовим числом n, просумуємо  по всі можливим значенням
по всі можливим значенням  :
:
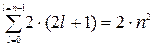
| (7.16) |
Таким чином, першому рівню енергії атома водню (n=1) відповідають два стани електрона, другому – 8, третьому –18 і т. д.
Стаціонарний квантовий стан електрона в атомі характеризується повним набором чотирьох квантових чисел: головного 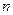 , орбітального
, орбітального  , магнітного m
, магнітного m 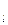 і спінового
і спінового 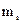 . Кожне з них характеризує квантування: енергії
. Кожне з них характеризує квантування: енергії 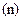 , моменту імпульсу
, моменту імпульсу 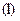 , його проекції на напрям зовнішнього магнітного поля
, його проекції на напрям зовнішнього магнітного поля  і проекції спіна
і проекції спіна 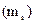 .
.
Для елементарних частинок, що мають спін рівний 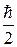 (електрони, протони, нейтрони та ін.) справедливий принцип Паулі: в будь – якій системі частинок із спіном
(електрони, протони, нейтрони та ін.) справедливий принцип Паулі: в будь – якій системі частинок із спіном 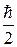 не може бути більше однієї частинки, що знаходиться в стаціонарному стані, який визначається повним набором чотирьох квантових чисел.
не може бути більше однієї частинки, що знаходиться в стаціонарному стані, який визначається повним набором чотирьох квантових чисел.
Якщо 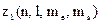 є число електронів в атомі, які знаходяться у стані, що визначається даним набором чотирьох квантових чисел, то
є число електронів в атомі, які знаходяться у стані, що визначається даним набором чотирьох квантових чисел, то 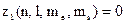 або 1.
або 1.
Найбільше число 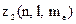 електронів в атомі, які знаходяться в станах, що визначаються набором трьох квантових чисел
електронів в атомі, які знаходяться в станах, що визначаються набором трьох квантових чисел 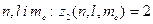
Найбільше число 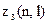
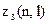 електронів в атомі, які знаходяться в станах, що визначаються набором двох квантових чисел
електронів в атомі, які знаходяться в станах, що визначаються набором двох квантових чисел 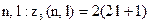 .
.
Найбільше число 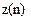 електронів в атомі, які знаходяться в станах, що визначаються значенням головного квантового числа
електронів в атомі, які знаходяться в станах, що визначаються значенням головного квантового числа 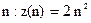 .
.
Дата добавления: 2015-06-01; просмотров: 1420;
