Автокорреляционная функция. Коррелограмма.
При наличии во временном ряду тенденции и циклических изменений значения последующего уровня ряда зависят от предыдущих. Зависимость между последовательными уровнями временного ряда называют автокорреляцией уровней ряда.
Количественно ее можно измерить с помощью индекса корреляции между уровнями исходного временного ряда и уровнями этого ряда, сдвинутыми на несколько шагов во времени.
Пусть задан временный ряд: у 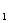 ,у,…у и пусть имеет место линейная корреляция между ytи yt-1.
,у,…у и пусть имеет место линейная корреляция между ytи yt-1.
Определим коэффициент корреляции между рядами уt и уt-1.
Для этого воспользуемся следующей формулой:
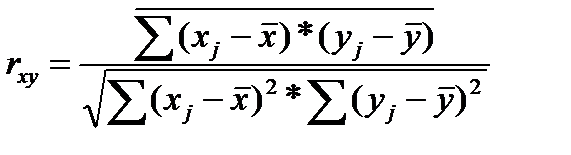
.
Пологая xj= уt-1, yj= уt-1, получим
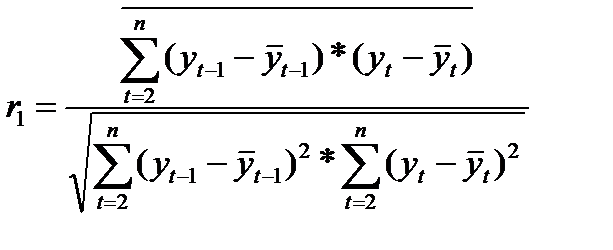 (5.1)
(5.1)
Аналогично определяются коэффициенты автокорреляции второго и более высоких порядков. Так, коэффициент автокорреляции 2-го порядка характеризует тесноту связи между уровнями у и у и определяется по формуле:
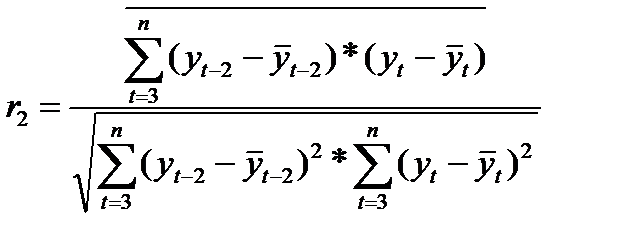 (5.2)
(5.2)
Порядок уровня ряда автокорреляции называют лагом.
Для формулы (5.1) лаг равен единице, для (5.3) –двум.
Последовательность коэффициентов автокорреляции уровней первого, второго и т.д. порядков называют автокорреляционной функцией временного ряда (АКФ).
График зависимости ее значений от величины лага называется коррелограмой.
АКФ и коррелограмма позволяют определить лаг, при котором автокорреляция наиболее высокая, а, следовательно, и лаг, при котором связь между текущим и предыдущим уровнями ряда наиболее тесная, т.е. с их помощью можно выявить структуру ряда.
Коэффициент автокорреляции и АКФ целесообразно использовать для выявления во временном ряде наличия или отсутствия трендовой компоненты и циклической компоненты:
если наиболее высоким оказался коэффициент автокорреляции 1-го порядка, то исследуемый ряд содержит только тенденцию;
если наиболее высоким оказался коэффициент автокорреляции к-го порядка, то ряд содержит циклические колебания с периодичностью в к-моментов времени;
если, ни один из коэффициентов не является значимым, то можно сделать одно из двух предположений, относительно структуры этого ряда: либо ряд не содержит тенденции и циклических изменений и имеет структуру, сходную со структурой ряда, изображенного на рис.5.1в, либо ряд содержит сильную нелинейную тенденцию, для выявления которой нужно провести дополнительный анализ.
49. Обобщенная модель регрессии. Обобщенный метод наименьших квадратов. Теорема Айткена
При построении модели, например, линейного вида
У = а + b1 * x1 + b2 * x2 +… + bp * xp + ε (59.1)
случайная величина представляет собой ненаблюдаемую величину. Для разных спецификаций модели разности 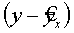 между теоретическими и фактическими значениями могут меняться. В задачу регрессионного анализа входит не только построение самой модели, но и исследование случайных отклонений i т.е. остаточных величин. После построения уравнения регрессии проводится проверка наличия у оценок i некоторых свойств. Эти свойства оценок, полученных МНК, имеют очень важное практическое значение в использовании результатов регрессии и корреляции.
между теоретическими и фактическими значениями могут меняться. В задачу регрессионного анализа входит не только построение самой модели, но и исследование случайных отклонений i т.е. остаточных величин. После построения уравнения регрессии проводится проверка наличия у оценок i некоторых свойств. Эти свойства оценок, полученных МНК, имеют очень важное практическое значение в использовании результатов регрессии и корреляции.
Коэффициенты регрессии bi, найденные на основе системы нормальных уравнений и представляющие собой выборочные оценки характеристики силы связи, должны обладать свойством несмещености. Несмещенность оценки означает, что математическое ожидание остатков равно нулю.
Это означает, что найденный параметр регрессии bi, можно рассматривать как среднее значение возможных значений коэффициентов регрессии с несмещенными оценками остатков.
Для практических целей важны не только несмещенность, но и эффективность оценок. Оценки считаются эффективными,если они характеризуются наименьшей дисперсией.
Для того, чтобы доверительные интервалы параметров регрессии были реальными, необходимо, чтобы оценки были состоятельными. Состоятельность оценок характеризует увеличение их точности с увеличением объема выборки.
Исследования остатков i предполагают проверку наличия следующих пяти предпосылок МНК:
случайный характер остатков;
нулевая средняя величина остатков, не зависящая от хi;
гомоскедастичность–дисперсия каждого отклонения i одинакова для всех значений х;
отсутствие автокорреляции остатков. Значения остатков i распределены независимо друг от друга;
остатки подчиняются нормальному распределению.
Если распределение случайных остатков i не соответствует некоторым предпосылкам МНК, то следует корректировать модель.
Прежде всего, проверяется случайный характер остатков i.
Если на графике получена горизонтальная полоса распределения остатков, то остатки представляют собой случайные величины и МНК оправдан, теоретические значения уx хорошо аппроксимируют фактические значения у.
Возможны следующие случаи: если i. зависит от уx то:
остатки i. не случайны
остатки i. не имеют постоянной дисперсии
остатки i. носят систематический характер
В этих случаях необходимо либо применить другую функцию, либо вводить дополнительную информацию и заново строить уравнение регрессии до тех пор, пока остатки i не будут случайными величинами.
Вторая предпосылка означает равенство нулю средней величины остатков:
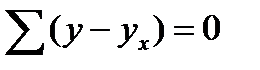 . (59.2)
. (59.2)
В соответствии с третьей предпосылкой МНК требуется, чтобы дисперсия остатков была гомоскедастичной. Это значит, что для каждого значения фактора хj остатки i имеют одинаковую дисперсию. Если это условие применения МНК не соблюдается, то имеет место гетероскедастичность.
50. Доступный обобщенный метод наименьших квадратов
Метод наименьших квадратов.Некоторые более общие типы регрессионных моделей рассмотрены в разделе Основные типы нелинейных моделей. После выбора модели возникает вопрос: каким образом можно оценить эти модели? Если вы знакомы с методами линейной регрессии (описанными в разделе Множественная регрессия) или дисперсионного анализа (описанными в разделе Дисперсионный анализ), то вы знаете, что все эти методы используют оценивание по методу наименьших квадратов. Основной смысл этого метода заключается в минимизации суммы квадратов отклонений наблюдаемых значений зависимой переменной от значений, предсказанных моделью. (Термин наименьшие квадраты впервые был использован в работе Лежандра - Legendre, 1805.)
Метод взвешенных наименьших квадратов. Третьим по распространенности методом, в дополнение к методу наименьших квадратов и использованию для оценивания суммы модулей отклонений (см. выше), является метод взвешенных наименьших квадратов. Обычный метод наименьших квадратов предполагает, что разброс остатков одинаковый при всех значениях независимых переменных. Иными словами, предполагается, что дисперсия ошибки при всех измерениях одинакова. Часто, это предположение не является реалистичным. В частности, отклонения от него встречаются в бизнесе, экономике, приложениях в биологии (отметим, что оценки параметров по методу взвешенных наименьших квадратов могут быть также получены с помощью модуля Множественная регрессия).
Например, вы хотите изучить связь между проектной стоимостью постройки здания и суммой реально потраченных средств. Это может оказаться полезным для получения оценки ожидаемых перерасходов. В этом случае разумно предположить, что абсолютная величина перерасходов (выраженная в долларах) пропорциональна стоимости проекта. Поэтому, для подбора линейной регрессионной модели следует использовать метод взвешенных наименьших квадратов. Функция потерь может быть, например, такой (см. книгу Neter, Wasserman, and Kutner, 1985, стр.168):
Потери = (наблюд.-предск.)2 * (1/x2)
В этом уравнении первая часть функции потерь означает стандартную функцию потерь для метода наименьших квадратов (наблюдаемые минус предсказанные в квадрате; т.е., квадрат остатков), а вторая равна “весу” этой потери в каждом конкретном случае - единица деленная на квадрат независимой переменной (x) для каждого наблюдения. В ситуации реального оценивания, программа просуммирует значения функции потерь по всем наблюдениям (например, конструкторским проектам), как описано выше и подберет параметры, минимизирующие сумму. Возвращаясь к рассмотренному примеру, чем больше проект (x), тем меньше для нас значит одна и та же ошибка в предсказании его стоимости. Этот метод дает более устойчивые оценки для параметров регрессии (более подробно, см. Neter, Wasserman, and Kutner. 1985).
51. Тест Чоу
Формальный статистический тест для оценки модели тенденции временного ряда при наличии структурных изменений был предложен Грегори Чоу*. Применение этого теста предполагает расчет параметров уравнений трендов. Введем систему обозначений, приведенную в табл.
Таблица 3 –Условные обозначения для алгоритма теста Чоу
| № уравнения | Вид уравнения | Число наблюдений в совокупности - | Остаточная сумма квадратов | Число параметров в уравнении | Число степеней свободы остаточной дисперсии |
| Кусочно –линейная модель | |||||
| 1) | У(1)=а1+b1t | n1 | C1ост | k1 | n1- k1 |
| 2) | У(2)=а2+b2t | n 2 | C2ост | k 2 | N2- k1 |
| Уравнение тренда по всей совокупности | |||||
| 3) | У(3)=а3+b3t | n | C3ост | k 3 |
Предположим, гипотеза Н0 утверждает структурную стабильность тенденции изучаемого временного ряда. Остаточную сумму квадратов по кусочно-линейной модели (Cклост) можно найти как сумму С1ост и C2ост
Cклост = С1ост + C2ост (62.1)
Соответствующее ей число степеней свободы составит:
(n1 - k1) + (n2 – k2) = n – k1 - k2 (62.2)
Тогда сокращение остаточной дисперсии при переходе единого уравнения тренда к кусочно-линейной модели определить следующим образом:
DСост = C3ост - Склост (62.3)
Число степеней свободы, соответствующее DС с учетом соотношения (23) составит:
n – k3 - (n – n1 – k2) = k1 + k2 - k3 (62.4)
Затем, в соответствии с Г. Чоу методикой Г. Чоу находится фактическое значение F-критерия по следующим дисперсиям на одну степень свободы вариации:
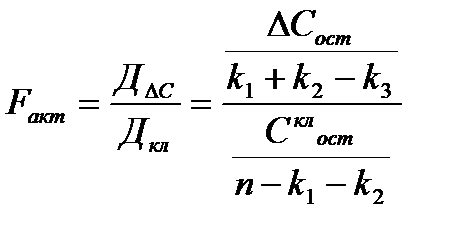 (62.5)
(62.5)
Найденное значение Fфакт сравнивают с табличным, (таблица распределения Фишера для уровня значимости α ‚ а и числа степеней свободы (k1+ k2 – k3) и (n - k1 - k2)
Если Fфакт > Fтабл‚ то гипотеза о структурной стабильности тенденции отклоняется, а влияние структурных измен на динамику изучаемого показателя признают значимым. В этом случае моделирование тенденции временного ряда следует произвести с помощью кусочно-линейной модели. Если
Fфакт < Fтабл то нулевая гипотеза структурной стабильности тенденции не отвергается. Ее моделирование следует осуществлять с помощью единого для всей совокупности уравнения тренда.
Особенности применения теста Чоу.
1. Если число параметров во всех уравнениях из таблицы 3 (1), (2), (3) одинаково и равно k, то формула (56) упрощается:
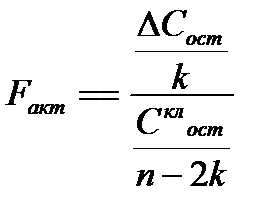 (62.6)
(62.6)
2. Тест Чоу позволяет сделать вывод о наличии или отсутствии структурной стабильности в изучаемом временном ряде. Если Fфакт < Fтабл , то это означает, что уравнения (1) и (2) описывают одну и ту же тенденцию, а различия численных оценок их пара метров а1 и а2 , а также b1 и b2 соответственно статистически не значимы. Если же Fфакт > Fтабл то гипотеза о структурной стабильности отклоняется, что означает статистическую значимость различий в оценках параметров уравнений (1) и (2).
З. Применение теста Чоу предполагает соблюдение предпосылок о нормальном распределении остатков в уравнениях (1) и (2) и независимость их распределений.
Если гипотеза о структурной стабильности тенденции ряда у, отклоняется, дальнейший анализ может заключаться в, исследовании вопроса о причинах этих структурных различий и более де 1 изучении характера изменения тенденции. В принятых обозначениях эти причины обусловливают различия в оценках параметров уравнений (1) и (2).
Возможны следующие сочетания изменений числейных оценок параметров этих уравнений :
• Изменение численной оценки свободного члена уравнения Тренда а2 по сравнению с а1 при условии, что различия b1 и b2 статистически незначимы. Геометрически это означает, что прямые (1) (2) параллельны. Происходит скачкообразное изменение уровня ряда уt, в момент времени t‚ и неизменном среднем абсолютном приросте за период;
• Изменение численной оценки параметра b2 по сравнению с b1 при условии, что различия между а1 и а2 статистически незначимы. Геометрически это означает, что прямые (1) и (2) пересекают ось координат в одной точке. Изменение тенденции происходит посредством изменение среднего абсолютного прироста временного ряда, начиная с момента времени t‚ при неизменном начальном уровне ряда в момент времени t =0
• Изменение численных оценок параметров а1 и а2, а так же b1 и b2 . На графике это отображается изменением начального уровня и счреднего за период абсолютного прироста
Дата добавления: 2015-05-21; просмотров: 6443;
