Доверительный интервал для оценки математического ожидания нормального распределения

Пусть случайная величина Х имеет нормальное распределение и известно ее среднее квадратическое отклонение 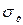. Требуется найти доверительный интервал, покрывающий математическое ожидание М_х с надежностью 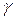, с учетом полученного значения выборочного среднего .

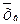Выборочная средняя является случайной величиной, поэтому ее можно обозначить .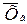

Опустив вывод формулы, запишем получившийся в результате интервал:

.

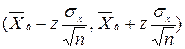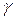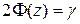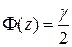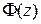Он покрывает неизвестное математическое ожидание М_х с надежностью . Число z определяем из выражения , т.е ( - функция Лапласа). По таблице функции Лапласа находим z, соответствующее значению .

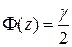Пример. Случайная величина Х имеет нормальное распределение с известным средним квадратичным отклонением 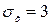. Найти доверительный интервал для оценки неизвестного математического ожидания по выборочному среднему 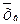, если объем выборки n=36, а надежность оценки .

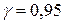Решение. Сначала находим z:

, ,

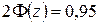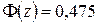По таблице функции Лапласа z=1,96. Затем определяем :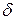

.

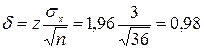Доверительный интервал запишем в виде

.

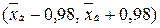При разных 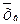границы интервала меняются.