Парциальные давления

Парциальное давление газа может быть определено через массовые доли из уравнения Клапейрона, если известны основные параметры газа:

(3-10)

Для нахождения парциального давления каждого газа при задании смеси объемными долями можно воспользоваться законом Бойля — Мариотта, из которого следует, что при постоянной температуре

(3-11)

Парциальное давление каждого газа равно произведению общего давления смеси газов на его объемную долю.

Уравнением (3-11) обычно пользуются при технических расчетах и при испытаниях тепловых установок. Объемные доли газов определяют специальными аппаратами — газоанализаторами.

Удельная энтальпия, т. е. энтальпия, отнесенная к 1 кг, обозначается буквой i и представляет собой по определению сложную функцию вида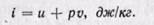

Дифференциал энтальпии di есть элементарное количество теплоты, участвующее в процессе при постоянном давлении. Вся теплота в процессе при постоянном давлении расходуется на изменение энтальпии:

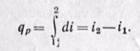(5-15)

Из уравнения (5-12) следует, что

(5-16)

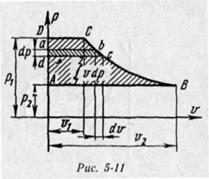
Энтальпия больше внешней теплоты на величину работы vdp, которая на рv-диаграмме изображается элементарной площадкой abed (рис. 5-11). Очевидно, вся пл. ABCD определяется выражением

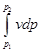, которое называется располагаемой, или полезной, работой.

Изменение энтальпии полностью определяется начальным и конечным состоянием рабочего тела и не зависит от промежуточных состояний. Изменение энтальпии газа в циклах равно нулю, т. е.

Поскольку энтальпия является функцией основных параметров состояния, то di есть полный дифференциал этой функции при любых независимых переменных, характеризующих состояние 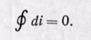газа;

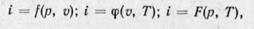
откуда

(5-17)

Изменение энтальпии во всех процессах, протекающих между двумя точками А и В, будет одинаковым (рис. 5-12).

Физический смысл энтальпии будет понятен из рассмотрения следующего примера. На перемещающийся поршень в цилиндре с 1 кг газа помещена гиря массой т кг (рис. 5-13). Площадь поршня /; внутренняя энергия рабочего тела и. Потенциальная энергия гири равна произведению массы гири т на высоту S. Так как давление газа р уравновешивается массой гири, то потенциальную энергию ее можно выразить иначе:

Произведение /S есть удельный объем газа. Отсюда

Произведение давления на объем есть работа, которую надо затратить, чтобы ввести газ объемом v во внешнюю среду с давлением р. Таким образом, работа pv есть потенциальная энергия газа, зависящая от сил, действующих на поршень. Чем больше эти внешние силы, тем больше давление р и тем больше потенциальная энергия давления pv.

Если рассматривать газ, находящийся в цилиндре и поршень с грузом как одну систему, которую будем называть расширенной системой, то полная энергия Е этой системы складывается из внутренней энергии газа и и потенциальной энергии поршня с грузом, равной pv:

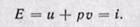(5-18)

Отсюда видно, что энтальпия i равна энергии расширенной системы — тела и окружающей среды. В этом и заключается физический смысл энтальпии.

Значения энтальпий для паров, газов и газовых смесей приводятся в технической и справочной литературе. Пользуясь этими данными, можно определять количество теплоты, участвующее в процессе при постоянном давлении. Энтальпия получила большое значение и применение при расчетах тепловых и холодильных установок и, как параметр состояния рабочего тела, значительно упрощает тепловые расчеты. Она позволяет [применять графические методы при исследовании всевозможных термодинамических процессов и циклов.

Энтальпией особенно целесообразно пользоваться тогда, когда в качестве основных параметров принимают р и Т. Это наглядно можно видеть, если энтальпию i сравнить с внутренней энергией и. При v = const уравнение первого закона термодинамики dq = = du + pdv превращается в dq_v = du, или q_v — u₂—u₁ а при р = const q_p = i₃ — i₁.

Энтальпия идеального газа,' так же как и внутренняя энергия, является функцией температуры и не зависит от других параметров. Действительно, для идеального газа

следовательно (поскольку оба слагаемых зависят только от температуры), i = f(T).

Тогда по аналогии с внутренней энергией будем иметь

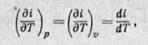(5-19)

т. е. в любом процессе изменения состояния идеального газа производная от изменения энтальпии по температуре будет полной производной.

Численные значения энтальпий идеальных газов приведены в приложении, табл. XIII.