Закони світлонадходження до приміщень

Аналіз залежності (1.19) дозволяє усвідомити, що освітленість у середині приміщення залежить від освітленості поза його межами. Щоб змоделювати і математично визначити такого роду залежність, розглянемо два закони світлонадходження до приміщень.

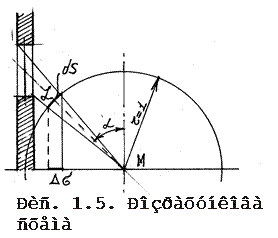
Перший закон – проекції тілесного кута. Він стверджує, що освітленість [27,29] у будь-якій точці приміщення, що створена рівномірно висвітлюючою поверхнею неба, прямо пропорційна яскравості неба і площі проекції тілесного кута променів від видимої ділянки неба на освітлювану поверхню.

Аналітичне доведення цього закону виконується за двома припущеннями:

1) освітлювана поверхня розташовується у приміщенні горизонтально;

2) радіус напівсфери має дорівнювати одиниці.

У такому випадку елементарна освітлюваність у точці М буде дорівнювати

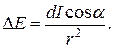(1.20)

Сила світла елементарної ділянки dS із заданою яскравістю L визначиться за формулою

dІ = LdS, (1.21)

у такому випадку при r = 1 елементарна освітленість стане рівною

DЕ = L×dS cos a.

Водночас проекція dS на горизонтальну поверхню дорівнює dσ = dS cosa, і тоді

DЕ = L dσ.

Інтегруючи обидві частини рівняння, одержуємо

Е = Lσ, лк. (1.22)

Тобто освітленість у будь-якій точці приміщення дорівнює добутку яскравості ділянки неба, яку видно із даної точки через вікно, на проекцію цієї ділянки неба (з r = 1) на освітлювану поверхню.

Якщо вибрати точку на горизонтальній поверхні під відкритим небосхилом, то освітленість у ній, згідно із законом, буде Е_н = Lpr², де pr² – площа проекції напівсфери на горизонтальну поверхню. Оскільки r = 1 , то Е_н = Lp. У такому випадку коефіцієнт природного освітлення у заданій точці М буде дорівнювати

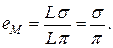(1.23)

Звідси видно, що коефіцієнт природного освітлення (КПО) у будь-якій точці поверхні визначається відношенням величини проекції видимої ділянки неба із точки до величини p (рівній 3,14). Це відношення являє собою геометричний зміст КПО.

Із використанням закону проекції тілесного кута стає можливим визначити відносну світлову активність різних світлопрорізів і порівнювати освітленості, створені одним і тим же світлопрорізом при різному розміщенні його відносно робочої поверхні. Цей закон дав змогу розробити графічні методи розрахунку природного освітлення. Зокрема, графічний спосіб розрахунку Данилюка розроблено на основі цього закону.

Другий закон – закон світлотехнічної подібності.

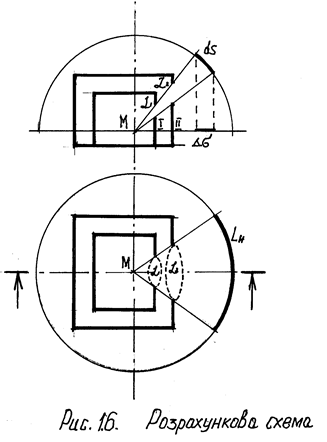Зміст цього закону пояснює схема, що наведена на рисунку 1.6. Освітленість у точці М створюється через вікна приміщення з яскравістю L₁ і L₂. Різна яскравість у цих вікнах може створюватися шляхом застосування різного скла. В іншому випадку вона може бути однаковою, тобто L₁ = L₂. Водночас зі схеми рисунка 1.6. видно, що освітленість у точці М створюється вікнами, що обмежені розмірами одного і того ж тілесного кута з вершиною у точці М. У такому випадку згідно зі змістом першого закону освітленість у точці М буде однаковою як при одному, так і при другому вікні, оскільки проекція тілесного кута на освітлювану площину буде незмінною і яскравість вікон збіжною (L₁ = L₂ = const). Таким чином, цей закон можна формулювати так: освітленість у точці приміщення буде однаковою, якщо вона створюється вікнами з однаковою яскравістю й однаковими тілесними кутами. Із цього закону випливає важливий висновок, що освітленість у точці приміщення залежить не від абсолютних, а від відносних розмірів вікна. Це має велике практичне значення, тому що дозволяє вивчати освітленість на моделях приміщень, дотримуючись при цьому точної масштабної і кольорової відповідності в опорядженні інтер’єрів, а для цього необхідно, щоб масштаб [29] моделі не був менший, ніж 1/20.

На основі цього закону можливо створювати не тільки моделі приміщень, але і модель штучного неба, що значно полегшує проблеми експериментального дослідження освітленості.