Дефекты в кристаллах

В реальных кристаллических решетках имеются отклонения от идеального порядка в расположении атомов, называемые дефектами решетки. Дефекты разделяют на макроскопическиеи микроскопические. К первым относятся, например, поры, трещины, инородные макроскопические включения. К микроскопическим дефектам относятся, например, вакансии (отсутствие атома в узле), внедрение атома в междуузельное пространство. Такие дефекты возникают и исчезают вследствие теплового движения атомов. Число микроскопических дефектов растет с ростом температуры кристалла.

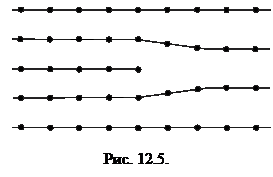Специфическими дефектами кристалли­ческой решетки являются дислокации– наруше­ния правильного порядка чередования атомных плоскостей, рис. 12.5. Наличие в кристалле дислокаций сильно влияет на его механические свойства. Если бы в металлах не было дислокаций, они были бы намного прочнее.

12.5. Теплоемкость кристаллов

При смещении атома в кристалле от положения равновесия - узла - на него действует со стороны других атомов возвращающая сила, которую при малых смещениях атомов, реально имеющих место при их тепловом движении, можно приближенно считать пропорциональной смещению, то есть упругой. Поэтому связь между атомами является квазиупругой, они как бы соединены друг с другом пружинками. Отсюда следует, что движение атомов в кристалле имеет характер малых гармонических колебаний, так что каждый атом кристалла является гармоническим осциллятором. Колебания атома не являются одномерными, то есть не происходят вдоль некоторой оси, а являются наложением колебаний, происходящих вдоль трех осей 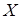, , 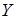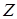. Таким образом, атом является трехмерным осциллятором и имеет три колебательных степени свободы. Поступательными степенями свободы атом не обладает. Вращательные степени свободы также следует исключить, если рассматривать атом как материальную точку. Итак, атом в узле кристаллической решетки имеет три степени свободы и все они являются колебательными. Один грамм-атом кристаллического вещества содержит 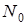атомов и, следовательно, имеет 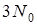степеней свободы. 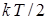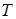Применяя классический закон равнораспределения, в соответствии с которым на каждую степень свободы системы, находящейся в равновесном состоянии, приходится в среднем кинетическая энергия , где - температура системы, заключаем, что кинетическая энергия колебательного движения 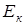атомов равна:

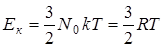. (12.1)

Потенциальная энергия упругого взаимодействия атомов в многоатомной молекуле равна их кинетической энергии, см. подраздел 6.1. Поскольку кристалл принципиально не отличается от многоатомной молекулы, то следует положить:

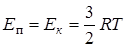, (12.2)

где 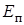- потенциальная энергия взаимодействия 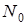атомов кристалла. Для внутренней энергии одного грамм-атома кристаллического вещества находим:

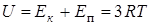. (12.3)

Подставляя (12.3) в формулу (6.25), получим молярную теплоемкость кристалла при постоянном объеме:

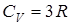. (12.4)

Формула (12.4) выражает закон Дюлонга и Пти, которые впервые экспериментально установили, что при «обычных» температурах теплоемкость кристаллов большинства химических элементов мало отличается от значения (12.4). Исключениями являются бериллий, алмаз и некоторые другие вещества, у которых молярная теплоемкость при обычных температурах значительно меньше, чем 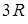и, кроме того, заметно зависит от температуры. Таким образом, закон Дюлонга-Пти имеет ограниченную область применения. Он не отражает также того факта, что при приближении температуры к абсолютному нулю теплоемкость кристаллов, как и всех других тел, стремится к нулю.

Ограниченность области примени­мости закона Дюлонга-Пти, вытекающего из классического закона равнораспре­деления, указывает на приближенный ха­рактер последнего.

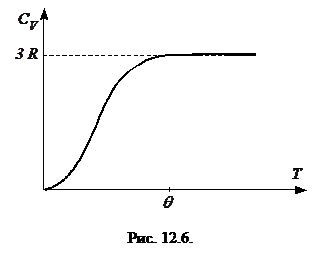
Хорошо согласуется с опытными дан­ными теория теплоемкости кристаллов, построенная Дебаем и основанная на кван­товых представлениях. Из теории Дебая, в частности, следует, что, начиная с неко­торой температуры 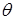, называемой харак­теристической температурой Дебая, теплоемкость начинает заметно убывать с понижением температуры и стремится к нулю при 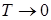. Примерный ход опыт­ной температурной зависимости молярной теплоемкости кристалла изображен на рис. 12.6.

Теплоемкости кристаллов при постоянном давлении и при постоянном объеме отличаются незначительно. Это обстоятельство связано с малостью коэффициента объемного расширения (теплового) твердых тел.