Метод Зейделя как модификация метода простой итерации
Метод Зейделя является более быстрой по сравнению с МПИ его модификацией.
Рассмотрим более подробно итерационную формулу (3) МПИ:
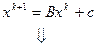
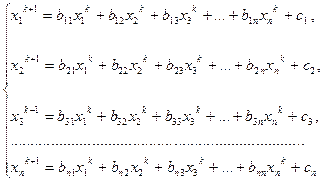 (6)
(6)
Здесь никакого значения не имеет порядок вычисления компонент вектора 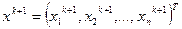 , не используются две возможности ускорения сходимости итерационного процесса.
, не используются две возможности ускорения сходимости итерационного процесса.
Первая возможность для ускорения состоит в том, чтобы только что вычисленные компоненты вектора 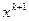 сразу же использовать для вычисления остальных компонент того же вектора
сразу же использовать для вычисления остальных компонент того же вектора 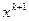 .
.
Вторая возможность (при использовании первой) состоит в изменении порядка вычисления компонент вектора 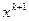 . Предположим, что выбран какой-то принцип, по которому выбирается порядок вычисления компонент
. Предположим, что выбран какой-то принцип, по которому выбирается порядок вычисления компонент 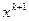 . Изменяя, если необходимо, порядок уравнений и неизвестных, можно считать, что уравнения для подстановки берутся в порядке возрастания их номеров. Для каждого итерационного шага может быть своя нумерация, т.е. перестановки должны быть выполнены при переходе от итерации к итерации (например, целесообразно первой всегда вычислять компоненту, у которой наибольшая погрешность).
. Изменяя, если необходимо, порядок уравнений и неизвестных, можно считать, что уравнения для подстановки берутся в порядке возрастания их номеров. Для каждого итерационного шага может быть своя нумерация, т.е. перестановки должны быть выполнены при переходе от итерации к итерации (например, целесообразно первой всегда вычислять компоненту, у которой наибольшая погрешность).
Для простоты далее рассматривается стационарный метод Зейделя, в котором порядок вычисления компонент не меняется.
Систему (6) запишем в виде:
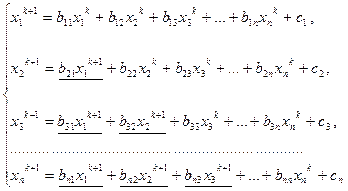 (7)
(7)
Метод, основанный на соотношениях (7), называется стационарным методом Зейделя. Это, как видно, модификация МПИ. За счет того, что вычисленные компоненты вектора 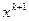 сразу же используются для вычисления его последующих компонент, вектор Зейделя сходится быстрее, чем МПИ, т.е. для достижения одной и той же заданной погрешности решения
сразу же используются для вычисления его последующих компонент, вектор Зейделя сходится быстрее, чем МПИ, т.е. для достижения одной и той же заданной погрешности решения 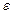 методу Зейделя потребуется меньше итераций, чем МПИ.
методу Зейделя потребуется меньше итераций, чем МПИ.
Дата добавления: 2015-03-20; просмотров: 1786;
