Координатных осей
Для пространственной системы сходящихся сил теорема Вариньона имеет вид: 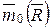 =
= 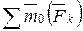 . Момент равнодействующей силы относительно точки равен векторной сумме моментов всех сил системы относительно той же точки. Если обе части векторного равенства спроецировать на ось z, проходящую через центр О, то получим:
. Момент равнодействующей силы относительно точки равен векторной сумме моментов всех сил системы относительно той же точки. Если обе части векторного равенства спроецировать на ось z, проходящую через центр О, то получим: 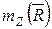 =
= 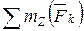 . Полученная формула есть теорема Вариньона относительно оси.
. Полученная формула есть теорема Вариньона относительно оси.
Разложим пространственную силу  , приложенную в точке А с координатами x, y, z, на составляющие
, приложенную в точке А с координатами x, y, z, на составляющие 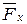 ,
, 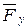 и
и 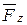 (рис.5.2). Тогда по теореме Вариньона:
(рис.5.2). Тогда по теореме Вариньона:  . Так как по свойству момента силы
. Так как по свойству момента силы 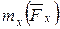 = 0, то получим:
= 0, то получим: 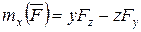 .
.
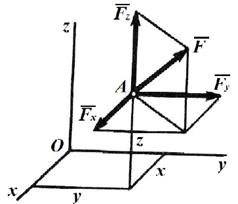
Рис. 5.2
Аналогично находятся моменты относительно осей y и z. Окончательно, получим:
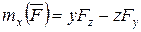 ;
; 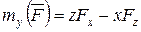 ;
; 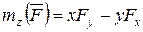 .
.
Полученные формулы есть аналитические формулы для моментов силы относительно координатных осей.
5.3. Задания для самостоятельной работы по теме «Момент силы относительно оси»
а)
Сила 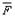 лежит в плоскости ABCD и приложена в точке В (рис. 5.3).
лежит в плоскости ABCD и приложена в точке В (рис. 5.3).
Момент силы 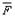 относительно оси ОZ равен...
относительно оси ОZ равен...
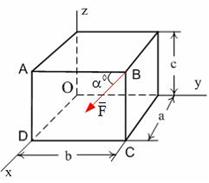 Рис. 5.3
Рис. 5.3
| Варианты ответов:

|
б)
Сила 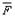 лежит в плоскости ABCD и приложена в точке В (рис. 5.4).
лежит в плоскости ABCD и приложена в точке В (рис. 5.4).
Момент силы 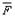 относительно оси ОY равен...
относительно оси ОY равен...
 Рис. 5.4
Рис. 5.4
| Варианты ответов:
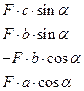
|
в)
Сила 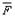 лежит в плоскости ABCD и приложена в точке В (рис. 5.5).
лежит в плоскости ABCD и приложена в точке В (рис. 5.5).
Момент силы 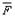 относительно оси ОZ равен...
относительно оси ОZ равен...
 Рис. 5.5
Рис. 5.5
| Варианты ответов:
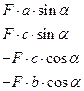
|
г)
Сила 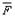 лежит в плоскости ABCD и приложена в точке D (рис. 5.6).
лежит в плоскости ABCD и приложена в точке D (рис. 5.6).
Момент силы 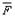 относительно оси ОZ равен…
относительно оси ОZ равен…
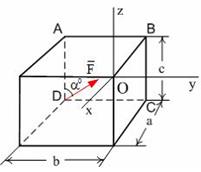 Рис. 5.6
Рис. 5.6
| Варианты ответов:
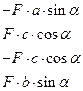
|
д)
Сила 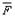 лежит в плоскости ABCD и приложена в точке A (рис. 5.7).
лежит в плоскости ABCD и приложена в точке A (рис. 5.7).
Момент силы 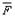 относительно оси ОY равен...
относительно оси ОY равен...
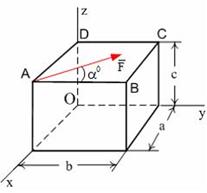 Рис. 5.7
Рис. 5.7
| Варианты ответов:
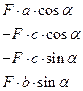
|
Дата добавления: 2015-03-17; просмотров: 1557;
