Спектральная плотность
В теории управления существуют и взаимно дополняют друг друга два подхода:
1) временнóй – исследование процессов во времени;
2) частотный – исследование частотных свойств сигналов и систем (с помощью передаточных функций и частотных характеристик).
Аналогичная ситуация наблюдается и при рассмотрении случайных процессов. Основная временная характеристика стационарного процесса – это корреляционная функция, а частотные свойства описываются спектральной плотностью.
Спектральная плотность – это функция, которая показывает распределение мощности сигнала по частотам. Такая информация о полезных сигналах, помехах и возмущениях очень важна для разработчика систем управления. Система должна быть спроектирована так, чтобы усиливать сигналы с «полезными» частотами и подавлять «вредные» частоты, характерные для помех и возмущений.
Для перехода от временнóго описания детерминированных (не случайных) процессов к частотному, используют преобразования Фурье и Лапласа. Аналогично спектральная плотность случайного процесса может быть найдена как преобразование Фурье от корреляционной функции[4]:
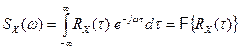 .
.
Здесь 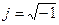 – мнимая единица, а
– мнимая единица, а 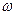 – угловая частота в рад/с (
– угловая частота в рад/с ( 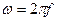 , где
, где 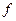 – «обычная» частота в герцах). Используя формулу Эйлера, можно представить экспоненту в виде сумму вещественной (косинусной) и мнимой (синусной) составляющих:
– «обычная» частота в герцах). Используя формулу Эйлера, можно представить экспоненту в виде сумму вещественной (косинусной) и мнимой (синусной) составляющих: 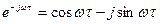 . Функция
. Функция 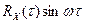 – нечетная по
– нечетная по 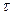 , поэтому интеграл от нее в симметричных пределах равен нулю. Напротив, функция
, поэтому интеграл от нее в симметричных пределах равен нулю. Напротив, функция 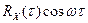 – четная, так что при интегрировании можно взять интервал от 0 до
– четная, так что при интегрировании можно взять интервал от 0 до 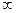 и удвоить результат:
и удвоить результат:
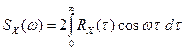 .
. 
(2)
Спектральная плотность чем-то похожа на плотность распределения вероятностей, только она характеризует плотность распределения мощности сигнала по частотам. Если случайный процесс – это напряжение в вольтах, то его корреляционная функция измеряется в В2, а спектральная плотность – в В2/Гц.
Спектральная плотность случайного процесса, имеющего корреляционную функцию 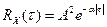 , вычисляется как
, вычисляется как
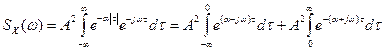 .
.
Интервал интегрирования разбит на две части. При 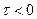 имеем
имеем 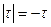 , а при
, а при 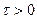 –
– 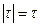 . Выполняя интегрирование, получаем
. Выполняя интегрирование, получаем
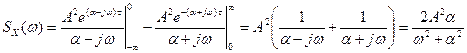 .
.
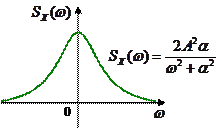
На рисунке слева показана корреляционная функция, а справа – соответствующая ей спектральная плотность мощности:
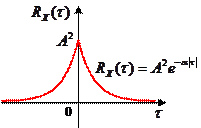
| 
|
Свойства спектральной плотности:
1) это неотрицательная, четная функция угловой частоты 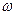 (график расположен выше оси абсцисс и симметричен относительно вертикальной оси);
(график расположен выше оси абсцисс и симметричен относительно вертикальной оси);
2) интеграл от 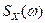 на некотором интервале частот
на некотором интервале частот 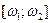 дает мощность, которая связана с этими частотами; поскольку функция
дает мощность, которая связана с этими частотами; поскольку функция 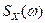 – четная, результат интегрирования на
– четная, результат интегрирования на 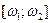 нужно удвоить, чтобы учесть также и полосу
нужно удвоить, чтобы учесть также и полосу 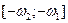 ;
;
3) площадь под кривой определяет средний квадрат случайного процесса (для центрированного процесса он равен дисперсии):
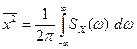 .
.
Множитель 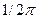 нужен для согласования единиц измерения, поскольку угловая частота
нужен для согласования единиц измерения, поскольку угловая частота 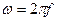 измеряется не в герцах, а в рад/с. Учитывая, что функция
измеряется не в герцах, а в рад/с. Учитывая, что функция 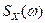 четная, можно интегрировать ее только при
четная, можно интегрировать ее только при 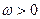 , а результат удвоить:
, а результат удвоить:
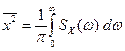 .
.
В теории управления нередко записывают спектральную плотность как функцию комплексной переменной 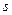 , связанной с угловой частотой по формуле
, связанной с угловой частотой по формуле 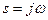 (отсюда следует
(отсюда следует 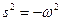 ). Хотя это не совсем корректно с точки зрения математики, мы будем использовать запись
). Хотя это не совсем корректно с точки зрения математики, мы будем использовать запись 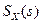 для обозначения спектральной плотности
для обозначения спектральной плотности 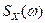 , в которой выполнена замена
, в которой выполнена замена 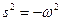 :
:
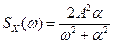
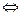
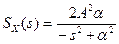 .
.
Дата добавления: 2014-12-09; просмотров: 9972;
